Que Son Las Medidas De Tendencia Central Media Mediana Moda

¡Hola a todos! Hoy hablaremos sobre las medidas de posición, de tendencia central y dispersión. Es muy importante entender estos términos para poder interpretar los datos estadísticos correctamente.

Medidas de posición

Las medidas de posición nos indican la posición relativa de un dato dentro de un conjunto de datos. Las más utilizadas son la mediana, el percentil y el cuartil.

Mediana

La mediana es el valor que ocupa la posición central en un conjunto de datos ordenados de menor a mayor. Si el conjunto de datos es par, se toma la media aritmética de los dos valores centrales.

Percentil

El percentil indica el porcentaje de datos que se encuentran por debajo del valor que estamos considerando. Por ejemplo, el percentil 25 indica que el 25% de los datos se encuentran por debajo de ese valor.

Cuartil

Los cuartiles dividen el conjunto de datos en cuatro partes iguales. El primer cuartil (Q1) señala el valor por debajo del cual se encuentra el 25% de los datos, el segundo cuartil (Q2), que es la mediana, el valor por debajo del cual se encuentra el 50% de los datos y el tercer cuartil (Q3), el valor por debajo del cual se encuentra el 75% de los datos.

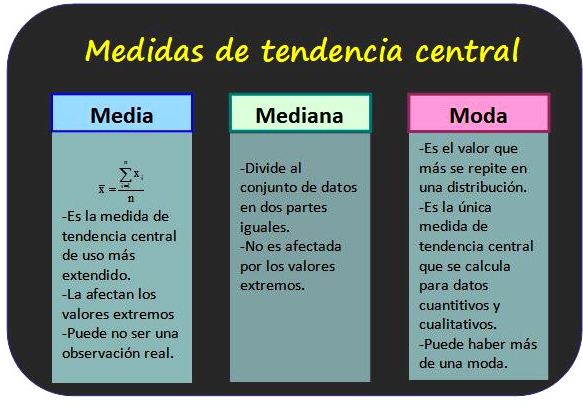
Medidas de tendencia central

Las medidas de tendencia central representan el valor que mejor resume un conjunto de datos. Las más utilizadas son la media, la mediana y la moda.

Media aritmética

La media es la suma de todos los valores dividida entre el número de valores. Es importante destacar que la media es muy sensible a los valores extremos (outliers).

Mediana

Como ya hemos mencionado, la mediana es el valor central en un conjunto de datos. A diferencia de la media, la mediana no se ve afectada por valores extremos.

Moda

La moda es el valor que más se repite en un conjunto de datos. Se puede tener varias modas o no tener ninguna.

Medidas de dispersión

Las medidas de dispersión nos indican cómo se distribuyen los datos alrededor de la medida de tendencia central. La más utilizada es la desviación estándar.

Desviación estándar

La desviación estándar indica cuánto se desvían los datos de la media. Si los datos tienen una desviación estándar baja, se encuentran muy cerca de la media. Si tienen una desviación estándar alta, se encuentran muy alejados de la media.

¿Cómo utilizar estas medidas?

Es importante entender que ninguna medida por sí sola es suficiente para interpretar un conjunto de datos. Es necesario analizar todas las medidas de posición, de tendencia central y de dispersión para poder obtener una imagen completa de la distribución de datos.

Por ejemplo, si tenemos un conjunto de datos con una media alta y una desviación estándar también alta, podemos concluir que los datos están bastante dispersos y que la media no representa adecuadamente la mayoría de los datos.

Consejos para interpretar estadísticas

Para interpretar adecuadamente las estadísticas es importante seguir estos consejos:

• Comprende el contexto: Es importante tener en cuenta el contexto en el que se generaron los datos. Por ejemplo, si estamos analizando los ingresos de una población, debemos tener en cuenta el país, el año y los factores socioeconómicos del lugar.
• Sé crítico: No te conformes con la primera conclusión que obtengas. Analiza cada medida y piensa en cuál es su verdadero significado.
• Compara y contrasta: Compara las diferentes medidas de posición, de tendencia central y de dispersión y contrasta con otros conjuntos de datos.
• Visualiza los datos: Muchas veces es más fácil interpretar los datos viéndolos en gráficas o diagramas.

Ideas equivocadas

Hay algunas ideas equivocadas sobre las medidas de tendencia central:

• La moda es siempre la medida más representativa. Esto no es cierto, depende del conjunto de datos.
• La media es siempre la mejor medida de tendencia central. Como ya hemos mencionado, la media es muy sensible a los valores extremos.

¿Cómo aprender más sobre estadísticas?

Si quieres aprender más sobre estadísticas, aquí te dejamos algunas recomendaciones:

• Cursos en línea: En la actualidad existen muchos cursos en línea gratuitos que puedes tomar para aprender más sobre estadísticas.
• Libros: Hay muchos libros sobre estadística, tanto para principiantes como para expertos. Busca uno que se ajuste a tus necesidades.
• Asesorías: Si necesitas ayuda para interpretar un conjunto de datos, siempre puedes acudir a un asesor o tutor.

Esperamos que esta introducción a las medidas de posición, de tendencia central y dispersión te haya resultado útil. ¡Hasta la próxima!