
¡Hola a todos! ¿Te encuentras en la búsqueda de información respecto a cómo calcular las medidas de tendencia central? Te traigo una variedad de ejercicios resueltos que te ayudarán a entender mejor esta herramienta estadística.
Table of Contents
Ejercicios Medidas de Tendencia Central
Comencemos con algunos ejercicios básicos para que entiendas cómo se calcula la media, mediana y moda.
La media es la suma de todos los valores, dividida por la cantidad de datos. Por ejemplo:
(4 + 6 + 2 + 8 + 3) / 5 = 4.6
Entonces, la media de este conjunto de datos es de 4.6
La mediana es el valor que se encuentra en el centro de los datos si los organizamos de menor a mayor. Por ejemplo:
2, 3, 4, 6, 8
La mediana en este caso es 4.
Por último, la moda es el valor que se repite con mayor frecuencia en un conjunto de datos. Por ejemplo:
2, 3, 4, 2, 6, 3, 2, 8, 2
La moda en este caso es 2, ya que aparece más veces que cualquier otro número.
MEDIA MODA MEDIANA EJERCICIOS RESUELTOS
Te mostrare algunos ejercicios ya resueltos para que puedas practicar y comprobar tus resultados.

En este ejemplo, se pide calcular la media y la mediana de un grupo de números. Los datos son:
10, 5, 2, 7, 9, 8, 6, 5, 7, 8, 6, 7, 3, 5, 9, 2, 1, 3, 6, 7
La media se calcula sumando todos los datos y dividiendo por la cantidad de ellos:
(10 + 5 + 2 + 7 + 9 + 8 + 6 + 5 + 7 + 8 + 6 + 7 + 3 + 5 + 9 + 2 + 1 + 3 + 6 + 7) / 20 = 5.65
La mediana se calcula ordenando los datos y escogiendo el valor que se encuentra en el centro. Como son 20 datos, el valor del centro está entre el décimo y el undécimo dato:
1, 2, 2, 3, 3, 5, 5, 5, 6, 6, 7, 7, 7, 8, 8, 9, 9, 10
La mediana es 6.5, ya que la suma de los dos valores del centro (6+7) dividida por dos es 6.5.
Cómo calcular medidas de tendencia central para datos estadísticos
Ahora, veremos cómo calcular las medidas de tendencia central en datos estadísticos.
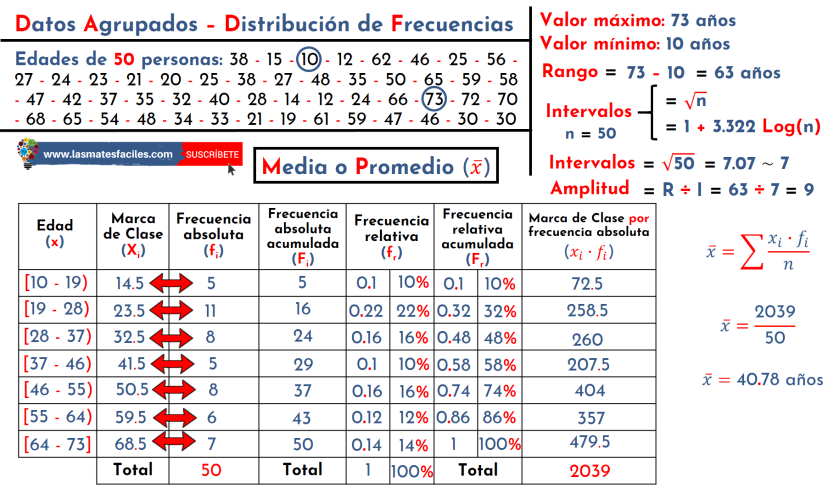
En una clasificación estadística podemos utilizar las medidas de tendencia central para comprender mejor los datos.
En este ejemplo, contamos con la siguiente tabla que nos muestra la cantidad de veces que se vendió un producto en un mes:
| Producto | Cantidad Vendida |
|---|---|
| Producto A | 50 |
| Producto B | 32 |
| Producto C | 28 |
| Producto D | 12 |
| Producto E | 7 |
Para calcular la media, sumamos la cantidad vendida de todos los productos y lo dividimos entre la cantidad de productos:
(50+32+28+12+7)/5 = 25,8
Entonces, la media de ventas de todos los productos es de 25,8.
La mediana se calcula encontrando el valor que se encuentra en el centro. Pero, primero debemos ordenar los datos de menor a mayor:
7, 12, 28, 32, 50
En este caso, la mediana es 28.
Finalmente, la moda es el valor que aparece con mayor frecuencia. En este caso, no hay un valor que se repita más veces que otro, por lo que no hay moda.
Ejercicios Resueltos Para Calcular La Media Mediana Y Moda
Realicemos algunos ejercicios más para practicar la capacidad de cálculo de las medidas de tendencia central.

En este ejemplo, debemos calcular la media, mediana y moda para el siguiente conjunto de datos:
4, 4, 4, 6, 6, 7, 8, 8, 10, 12, 12, 14, 14, 14
La media se calcula sumando todos los números y dividiéndolo por la cantidad de ellos:
(4+4+4+6+6+7+8+8+10+12+12+14+14+14)/14=9
La mediana es el valor que se encuentra en el centro. Como hay 14 datos, el séptimo y el octavo dato son los del centro:
4, 4, 4, 6, 6, 7, 8, 8, 10, 12, 12, 14, 14, 14
La mediana es 8.
Por último, la moda es el valor que se repite con mayor frecuencia. En este caso, la moda es 4 y 14, ya que ambos valores aparecen tres veces.
Ejercicios Medidas De Tendencia Central – Estudiar
En este ejercicio, debemos calcular la media, mediana y moda para el siguiente conjunto de datos:
10, 20, 30, 40, 50, 60, 70

La media se calcula sumando todos los datos y después dividiéndolos entre la cantidad de datos:
(10+20+30+40+50+60+70)/7 = 40
La mediana es el valor que se encuentra en el centro. Como el total de datos es un número impar, la mediana es el valor que se encuentra en la posición número cuatro, que es 40.
Por último, la moda se refiere al valor que se repite con mayor frecuencia en un conjunto de datos. En este caso, no existe moda ya que ningún valor se repite más de una vez.
florero Jardines Precaución tendencia central media mediana y moda
En este último ejercicio, vamos a calcular la media, mediana y moda para el conjunto de datos:
2, 2, 2, 4, 4, 6, 8, 8, 10, 10, 10, 12, 12, 12, 14, 14, 16, 18, 18, 20

La media se calcula sumando todos los datos y dividiendo entre la cantidad de datos:
(2+2+2+4+4+6+8+8+10+10+10+12+12+12+14+14+16+18+18+20) /20 = 10
La mediana es el valor que se encuentra en el centro. Como hay 20 datos, los valores del centro se encuentran entre los décimo y el undécimo dato:
2, 2, 2, 4, 4, 6, 8, 8, 10, 10, 10, 12, 12, 12, 14, 14, 16, 18, 18, 20
La mediana es 11 ya que es la media de los dos valores del centro (10 + 12)/2.
Finalmente, la moda se refiere al valor que se repite más frecuentemente en un conjunto de datos. En este caso, la moda es 10, ya que es el valor que más se repite.
Espero que estos ejercicios te hayan sido de ayuda en la comprensión de las medidas de tendencia central. Recuerda que estas son herramientas importantes de la estadística y te ayudarán a entender mejor los datos. ¡Así que súmate a la aventura de los números y sigue aprendiendo!
 Moda y Estilo Las mejores ideas de Estilo de moda
Moda y Estilo Las mejores ideas de Estilo de moda


