¡Hola a todos! Hoy vamos a hablar sobre un tema muy importante en la estadística: las medidas de tendencia central. Seguro que si habéis estudiado esta rama de las matemáticas, habéis oído hablar de la media, la mediana y la moda. En este artículo, vamos a profundizar en estas tres medidas y a daros algunos consejos e ideas para entenderlas y utilizarlas correctamente.
Table of Contents
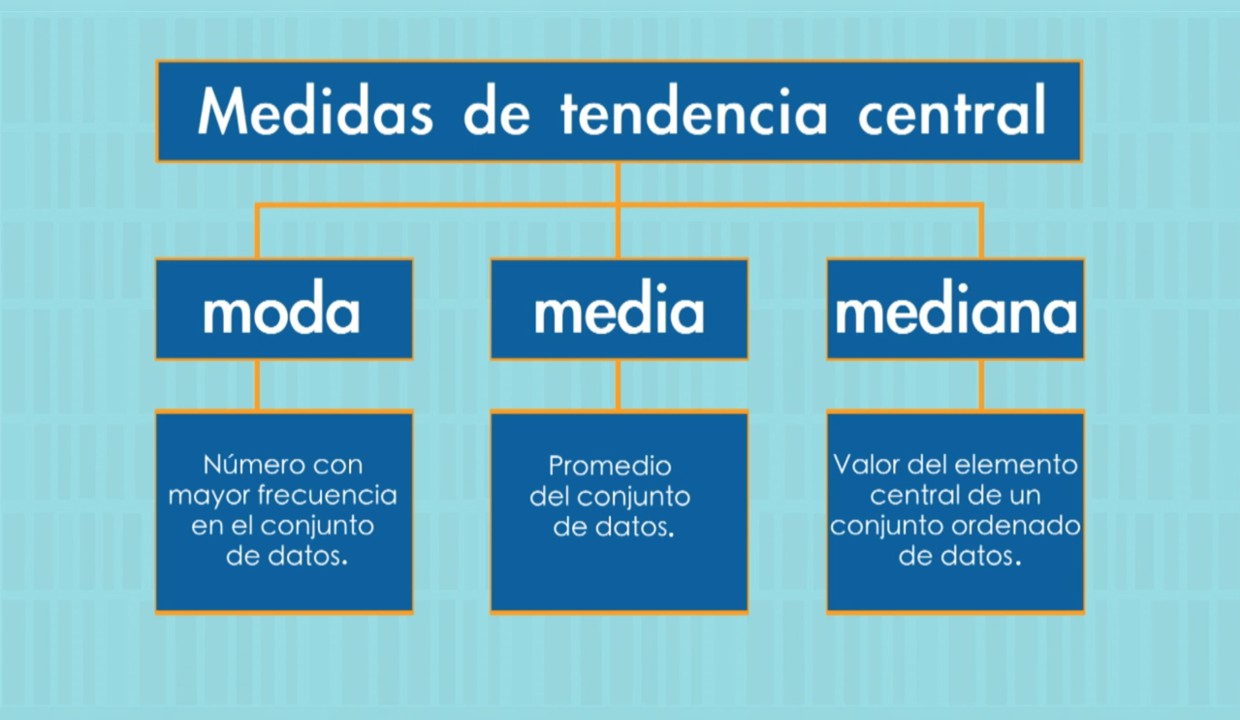
La media
La media, también conocida como promedio, es la suma de todos los valores de una distribución dividida entre el número total de valores. Veamos un ejemplo:
En este ejemplo, tenemos una distribución de notas de un examen con un total de 10 alumnos. Para calcular la media, sumamos todas las notas y las dividimos entre 10:
Media = (5 + 6 + 7 + 8 + 9 + 5 + 7 + 8 + 9 + 10) / 10 = 7.4
Es decir, la media de esta distribución de notas es 7.4.
La media tiene la ventaja de que es fácil de calcular y suele ser una buena representación del centro de la distribución. Sin embargo, tiene el inconveniente de que puede verse muy influenciada por valores atípicos o extremos. Por ejemplo, si alguien saca un 1 en el examen anterior, la media bajaría bastante aunque el resto de los alumnos hayan sacado buenas notas.
La mediana
La mediana es el valor que se encuentra en el centro de una distribución. Para calcularla, es necesario ordenar todos los valores de la distribución de menor a mayor y buscar el valor que ocupa la posición central. Veamos el mismo ejemplo que antes:

En este caso, ordenamos las notas de menor a mayor:
5, 5, 6, 7, 7, 8, 8, 9, 9, 10
La mediana de esta distribución sería el valor que ocupa la posición central, es decir, el valor número 5:
Mediana = 7
La mediana tiene la ventaja de que no se ve afectada por valores atípicos o extremos, ya que solo tiene en cuenta el valor central. Sin embargo, puede ser difícil de calcular en distribuciones con un gran número de valores o con valores repetidos.
La moda
La moda es el valor que más se repite en una distribución. En el mismo ejemplo de antes, la moda sería el número 5, ya que aparece dos veces:

La moda tiene la ventaja de ser muy fácil de calcular y de proporcionarnos información sobre el valor más común o frecuente de una distribución. Sin embargo, a diferencia de la media y la mediana, no nos da información sobre el centro de la distribución, ya que puede haber varias modas o incluso ninguna.
Es importante recordar que estas tres medidas de tendencia central solo nos dan información sobre un aspecto de la distribución. Para tener una visión más completa, es recomendable utilizar otras medidas estadísticas como la desviación estándar, el rango intercuartílico o el coeficiente de variación.
Consejos
Para utilizar correctamente las medidas de tendencia central, ten en cuenta estos consejos:
- No te limites a utilizar solo una medida. Es recomendable utilizar varias para tener una visión más completa de la distribución.
- Ten en cuenta los valores atípicos o extremos y cómo pueden afectar a la interpretación de las medidas.
- Utiliza las medidas de tendencia central adecuadas según el tipo de variable que estés analizando. Por ejemplo, la moda no tiene sentido para variables continuas.
- No olvides que las medidas de tendencia central no lo son todo. Utiliza otras medidas estadísticas para tener una visión más completa de la distribución.
Ideas para practicar
Para entender mejor las medidas de tendencia central, te proponemos las siguientes ideas:

- Toma una muestra aleatoria de valores y calcula su media, mediana y moda.
- Cambia uno o varios valores extremos de la muestra anterior y vuelve a calcular las medidas de tendencia central.
- Crea una tabla con varios valores repetidos y trata de calcular la mediana.
- Busca ejemplos de distribuciones asimétricas y estudia cómo afectan las medidas de tendencia central a su interpretación.
Cómo utilizar las medidas de tendencia central en análisis de datos
Las medidas de tendencia central son una herramienta fundamental en el análisis de datos. Para utilizarlas correctamente en este contexto, te proponemos los siguientes pasos:
- Recopila los datos que vas a analizar y ordénalos adecuadamente.
- Calcula las medidas de tendencia central (media, mediana, moda) y otras medidas estadísticas relevantes (desviación estándar, rango intercuartílico, coeficiente de variación).
- Interpreta las medidas obtenidas y utiliza gráficos para visualizar la distribución de los datos (histogramas, diagramas de caja, diagramas de dispersión).
- Trata de encontrar patrones y relaciones entre los datos y utiliza las medidas de tendencia central para apoyar tus conclusiones.
- Considera las limitaciones y debilidades de las medidas de tendencia central y utiliza otras medidas estadísticas si es necesario.
En resumen, las medidas de tendencia central son una herramienta fundamental en la estadística y en el análisis de datos. Esperamos que esta guía te haya ayudado a entender mejor estas medidas y a utilizarlas con mayor eficacia en tus trabajos y proyectos. ¡Sigue practicando y aprendiendo!
 Moda y Estilo Las mejores ideas de Estilo de moda
Moda y Estilo Las mejores ideas de Estilo de moda


