3.2 Medidas De Tendencia Media Mediana Moda Promedio

¡Hola amigos! Hoy quiero hablarles sobre un tema muy interesante y útil en la estadística: las medidas de tendencia central. Esta herramienta nos permite conocer la posición central de un conjunto de datos, lo que nos ayuda a interpretarlos mejor y sacar conclusiones más precisas. En este post les explicaré qué son la media, la mediana y la moda, cómo se calculan y cómo se utilizan para analizar datos.

Media

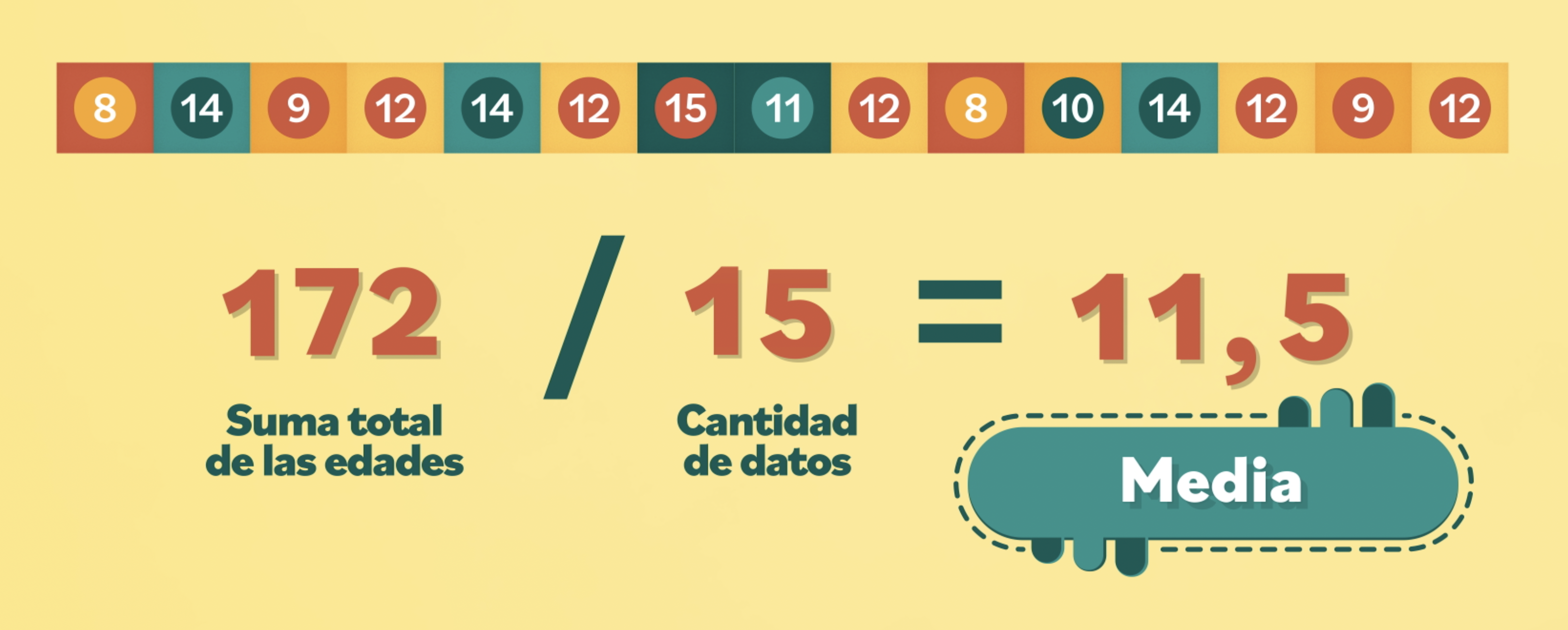
La media es el valor obtenido al dividir la suma de todos los datos entre el número de datos. Es decir, si tenemos 4 números (a, b, c y d), la media sería: (a + b + c + d) / 4. La media nos indica el valor promedio de los datos, por lo que si tenemos una distribución simétrica, será el valor del centro. La media también es muy sensible a los valores extremos, por lo que si tenemos un valor muy alto o muy bajo, puede afectar significativamente el resultado.

Consejos:

• Para calcular la media, es importante tener en cuenta todos los datos y no omitir ninguno.
• Si tenemos valores extremos que afectan demasiado el resultado, podemos utilizar la media recortada, que consiste en eliminar un cierto porcentaje de los valores más altos y más bajos antes de calcular la media.

Mediana

La mediana es el valor central de un conjunto de datos ordenados de menor a mayor. Por ejemplo, si tenemos los números 1, 3, 5, 7 y 9, la mediana sería 5, ya que es el valor central. Si tenemos un número par de datos, se toma la media de los dos valores centrales. La mediana es menos sensible a los valores extremos que la media, por lo que es una medida más robusta.

Ideas:

• Para calcular la mediana, es necesario ordenar los datos de menor a mayor (o viceversa).
• La mediana es útil cuando tenemos valores extremos o datos que no siguen una distribución normal.

Moda

La moda es el valor que ocurre con mayor frecuencia en un conjunto de datos. Es decir, es el valor que “más se repite”. Si todos los valores ocurren con la misma frecuencia, entonces no hay moda. La moda es útil para identificar los valores más comunes y para obtener información sobre la forma y la simetría de la distribución.

Como:

• Para calcular la moda, es necesario identificar el valor que se repite con mayor frecuencia en los datos.
• Si hay más de una moda (es decir, varios valores que se repiten con la misma frecuencia máxima), entonces hay una distribución bimodal o multimodal.

Aplicaciones

Las medidas de tendencia central son muy útiles en la vida cotidiana y en diversas áreas del conocimiento. Por ejemplo, en economía se utilizan para analizar la distribución de ingresos o precios, en medicina se utilizan para estudiar la efectividad de un tratamiento o para determinar los valores normales de una prueba de laboratorio, en psicología se utilizan para medir la inteligencia o la personalidad, entre otras aplicaciones.

Consejos:

• Es importante entender el contexto de los datos y cómo se han obtenido antes de calcular las medidas de tendencia central.
• No hay una medida de tendencia central “mejor” o “peor”, sino que cada una tiene sus ventajas y desventajas según la situación.

En resumen, las medidas de tendencia central son una herramienta muy útil para interpretar los datos y sacar conclusiones más precisas. La media nos indica el valor promedio de los datos, la mediana nos indica el valor central y la moda nos indica el valor más común. Es importante conocer y utilizar estas medidas correctamente para obtener información valiosa en diversos campos. Espero que este post les haya sido útil y les haya permitido entender mejor el mundo de la estadística. ¡Hasta la próxima!