Concepto De Moda En Medidas De Tendencia Central

En el mundo de la estadística, las medidas de tendencia central juegan un papel crucial. Son herramientas que permiten a los expertos analizar y comprender mejor los datos que se presentan ante ellos. En este post hablaremos de las principales medidas de tendencia central: la media, la moda y la mediana.

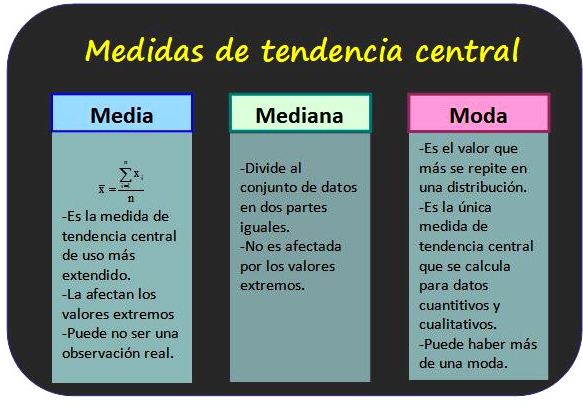
La media

La media es la medida de tendencia central más comúnmente utilizada en la estadística. Se calcula sumando todos los valores de una muestra y dividiendo el resultado entre el número total de elementos en la misma.

Con la media podemos obtener una idea de la tendencia general de los datos. Si la media es mayor que la mediana, significa que hay valores que están por encima del promedio y estos valores podrían estar sesgando los resultados. Por el contrario, si la media es menor que la mediana, indica que existen valores que están por debajo del promedio, lo que indica una posible falta de precisión en los datos.

La moda

La moda es el valor que se repite con mayor frecuencia en una muestra de datos. Esta medida de tendencia central se utiliza para analizar las tendencias en la distribución de los valores. Si la moda y la media son cercanas, significa que la distribución de los datos es simétrica y centrada alrededor del valor medio. Si la moda está desplazada a la izquierda o a la derecha de la media, se podría inferir que los datos están sesgados hacia un lado.

Es importante tener en cuenta que una muestra puede tener más de una moda y esto es conocido como una distribución bimodal.

La mediana

La mediana es el valor que ocupa la posición central en una muestra cuando se dispone en orden creciente o decreciente. Si el número de elementos en la muestra es par, la mediana es el promedio de los dos valores centrales. La mediana es útil en casos de datos extremos que pueden afectar la media. También es especialmente útil para datos que no se distribuyen normalmente.

Consejos para utilizar las medidas de tendencia central

Para utilizar las medidas de tendencia central de manera efectiva, es importante tener en cuenta algunos consejos:

• Revisar los gráficos de los datos antes del cálculo de las medidas para entender las tendencias generales (en la forma del gráfico, si hay picos o valles importantes, si hay asimetría).
• Verificar si los datos están sesgados, en cuyo caso, utilizar medianas.
• Verificar si hay valores atípicos, en cuyo caso, utilizar medianas.
• Asegurarse de que las medidas se manejen juntas con otras medidas de dispersión de datos, para que se puedan tener una comprensión más precisa y completa.

Ideas para utilizar las medidas de tendencia central en la vida diaria

Las medidas de tendencia central se utilizan en una gran cantidad de situaciones cotidianas. Algunas ideas para utilizarlas son:

• En el análisis de resultados de ventas, para entender el comportamiento de los clientes.
• En el análisis de encuestas, para entender las tendencias de opinión pública y política.
• En la evaluación de resultados financieros, para entender la tendencia de una empresa en su mercado.
• En la evaluación de la evolución de los precios de productos o servicios, para entender la tendencia de los mismos en el mercado.

Cómo calcular las medidas de tendencia central

Si bien existen aplicaciones específicas para el cálculo de las medidas de tendencia central, también se pueden calcular manualmente en una hoja de cálculo. El proceso para calcular cada una es el siguiente:

Media:

1. Sumar todos los elementos en la muestra.
2. Dividir el resultado de la suma entre el número total de elementos en la muestra.

Moda:

1. Encontrar el valor que aparece con mayor frecuencia en la muestra.

Mediana:

1. Ordenar los elementos de menor a mayor.
2. Si la cantidad de elementos es impar, el número en la posición central es la mediana.
3. Si la cantidad de elementos es par, la mediana es el promedio de los dos valores centrales.

Conclusión

Las medidas de tendencia central son herramientas muy útiles para analizar y comprender mejor los datos. La media, la moda y la mediana son las medidas más comúnmente utilizadas y cada una se puede utilizar en diferentes situaciones. Para utilizar las medidas de tendencia central de manera efectiva, es importante tener en cuenta algunos consejos y consideraciones, y para calcularlas se puede utilizar una hoja de cálculo o aplicaciones específicas de estadística.

Esperamos que este artículo te haya ayudado a comprender mejor la importancia de estas medidas en la estadística.

Fuentes

• “Aplicaciones estadísticas del cálculo fraccionario: Promedio y mediana” de feyalegria.edu.pe
• “ESTADÍGRAFOS – Mind Map”, de aprendiendoadministracion.com
• “fútbol americano Caracterizar Hablar concepto de media moda y mediana” de youtube.com
• “Medidas de posición, de tendencia central y dispersión (2022)” de lifeder.com
• “5.medidas de tendencia central” de slidesharecdn.com
• “Profesor Julio Cesar Sandino: medidas de tendencia central para datos” de blogspot.com

Las imágenes utilizadas en este artículo son propiedad de sus respectivos dueños.