
Hola a todos!
Table of Contents
Medidas de Tendencia Central en Estadística
La estadística es una rama de las matemáticas que se ocupa de recopilar, interpretar y analizar datos relacionados con una población o muestra. Una de las técnicas estadísticas más utilizadas es la medición de la tendencia central, que es una medida que representa el valor central o típico de un conjunto de datos.
En este post, vamos a hablar sobre las medidas de tendencia central y su importancia en la estadística. También vamos a dar algunos consejos y sugerencias sobre cómo utilizar estas medidas para entender mejor los datos y tomar decisiones informadas.
Medias de Tendencia Central
En estadística, las medidas de tendencia central se refieren a un valor único que se utiliza como un representante del conjunto de datos. Las tres medidas de tendencia central más comunes son la media aritmética, la mediana y la moda.
Media Aritmética
La media aritmética es la más utilizada y conocida de las tres medidas de tendencia central. Para calcular la media aritmética, simplemente sumamos todos los valores en el conjunto de datos y dividimos por el número total de valores.
Por ejemplo, si tenemos los siguientes números: 5, 10, 15, 20, 25, la media aritmética sería:
(5 + 10 + 15 + 20 + 25) / 5 = 15
Por lo tanto, la media aritmética de estos números es 15.
Mediana
La mediana es el valor que se encuentra en la mitad de un conjunto de datos ordenados en orden ascendente o descendente. Si el conjunto de datos tiene un número impar de valores, la mediana es el valor medio exactamente. Si el conjunto de datos tiene un número par de valores, la mediana es la media aritmética de los dos valores centrales.
Por ejemplo, si tenemos los siguientes números: 5, 10, 15, 20, 25, la mediana sería:
15
Por lo tanto, la mediana de estos números es 15.
Moda
La moda es el valor más común en un conjunto de datos. En otras palabras, la moda es el valor que aparece más frecuentemente.
Por ejemplo, si tenemos los siguientes números: 5, 10, 15, 15, 20, 25, la moda sería:
15
Por lo tanto, la moda de estos números es 15.
Cómo utilizar las medidas de tendencia central
Ahora que sabemos qué son las medidas de tendencia central, es importante saber cómo utilizarlas para entender mejor los datos.
Consejos
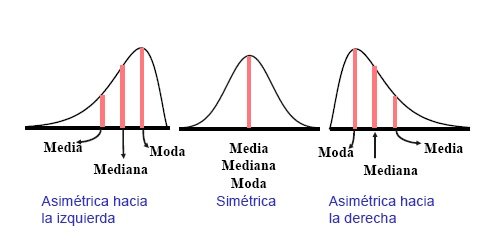
Uno de los mejores consejos es utilizar más de una medida de tendencia central. Por ejemplo, si usamos la media aritmética y la mediana, podemos tener una mejor comprensión del conjunto de datos. Si los valores son similares, significa que los datos son simétricos y están bien distribuidos. Si no, el conjunto de datos puede estar sesgado hacia los valores extremos, lo que significa que algunos valores tienen una mayor influencia en la media aritmética.
Otro consejo es no utilizar la moda como única medida, ya que no siempre refleja adecuadamente la naturaleza del conjunto de datos. Si tenemos un conjunto de datos en el que todos los valores son diferentes, no hay modo. Alternativamente, si hay más de una moda, el conjunto de datos puede estar formado por dos o más grupos diferentes de datos.
Ideas
La medida de la tendencia central que es más adecuada para un conjunto de datos depende del tipo de datos. Por ejemplo, si tenemos datos nominales o categóricos, la moda es una buena medida de tendencia central. Si los datos son continuos, la media aritmética y la mediana son más adecuadas.
Otra idea es utilizar las medidas de tendencia central en conjunción con otras medidas estadísticas, como la desviación estándar y la varianza, para obtener una comprensión más completa de los datos. Por ejemplo, si la media aritmética es 80 y la desviación estándar es 10, podemos inferir que la mayoría de los valores están cerca de 80 y que hay menos valores que están más alejados de la media.
Cómo
En términos de cálculo de medidas de tendencia central, existen varias fórmulas. La más común es:
Media = suma de los valores / número de valores
Mediana = valor en la mitad del conjunto de datos
Moda = valor que aparece más frecuentemente
Hay también otras fórmulas para calcular estas medidas, como la media ponderada y la mediana ponderada, pero son menos comunes.
En conclusión, las medidas de tendencia central son útiles para entender mejor los datos y tomar decisiones informadas. La media aritmética, la mediana y la moda son las medidas más comunes, y es importante tener en cuenta que la medida adecuada depende del tipo de datos y de los objetivos del análisis. Para obtener una comprensión más completa de los datos, se pueden utilizar varias medidas de tendencia central junto con otras medidas estadísticas.
Esperamos que este post os haya resultado útil e interesante. ¡Hasta la próxima!

Medidas de Tendencia Central en Estadística
La estadística es una rama de las matemáticas que se ocupa de recopilar, interpretar y analizar datos relacionados con una población o muestra. Una de las técnicas estadísticas más utilizadas es la medición de la tendencia central, que es una medida que representa el valor central o típico de un conjunto de datos.
En este post, vamos a hablar sobre las medidas de tendencia central y su importancia en la estadística. También vamos a dar algunos consejos y sugerencias sobre cómo utilizar estas medidas para entender mejor los datos y tomar decisiones informadas.
Medias de Tendencia Central
En estadística, las medidas de tendencia central se refieren a un valor único que se utiliza como un representante del conjunto de datos. Las tres medidas de tendencia central más comunes son la media aritmética, la mediana y la moda.
Media Aritmética
La media aritmética es la más utilizada y conocida de las tres medidas de tendencia central. Para calcular la media aritmética, simplemente sumamos todos los valores en el conjunto de datos y dividimos por el número total de valores.
Por ejemplo, si tenemos los siguientes números: 5, 10, 15, 20, 25, la media aritmética sería:
(5 + 10 + 15 + 20 + 25) / 5 = 15
Por lo tanto, la media aritmética de estos números es 15.
Mediana
La mediana es el valor que se encuentra en la mitad de un conjunto de datos ordenados en orden ascendente o descendente. Si el conjunto de datos tiene un número impar de valores, la mediana es el valor medio exactamente. Si el conjunto de datos tiene un número par de valores, la mediana es la media aritmética de los dos valores centrales.
Por ejemplo, si tenemos los siguientes números: 5, 10, 15, 20, 25, la mediana sería:
15
Por lo tanto, la mediana de estos números es 15.
Moda
La moda es el valor más común en un conjunto de datos. En otras palabras, la moda es el valor que aparece más frecuentemente.
Por ejemplo, si tenemos los siguientes números: 5, 10, 15, 15, 20, 25, la moda sería:
15
Por lo tanto, la moda de estos números es 15.
Cómo utilizar las medidas de tendencia central
Ahora que sabemos qué son las medidas de tendencia central, es importante saber cómo utilizarlas para entender mejor los datos.
Consejos
Uno de los mejores consejos es utilizar más de una medida de tendencia central. Por ejemplo, si usamos la media aritmética y la mediana, podemos tener una mejor comprensión del conjunto de datos. Si los valores son similares, significa que los datos son simétricos y están bien distribuidos. Si no, el conjunto de datos puede estar sesgado hacia los valores extremos, lo que significa que algunos valores tienen una mayor influencia en la media aritmética.
Otro consejo es no utilizar la moda como única medida, ya que no siempre refleja adecuadamente la naturaleza del conjunto de datos. Si tenemos un conjunto de datos en el que todos los valores son diferentes, no hay modo. Alternativamente, si hay más de una moda, el conjunto de datos puede estar formado por dos o más grupos diferentes de datos.
Ideas
La medida de la tendencia central que es más adecuada para un conjunto de datos depende del tipo de datos. Por ejemplo, si tenemos datos nominales o categóricos, la moda es una buena medida de tendencia central. Si los datos son continuos, la media aritmética y la mediana son más adecuadas.
Otra idea es utilizar las medidas de tendencia central en conjunción con otras medidas estadísticas, como la desviación estándar y la varianza, para obtener una comprensión más completa de los datos. Por ejemplo, si la media aritmética es 80 y la desviación estándar es 10, podemos inferir que la mayoría de los valores están cerca de 80 y que hay menos valores que están más alejados de la media.
Cómo
En términos de cálculo de medidas de tendencia central, existen varias fórmulas. La más común es:
Media = suma de los valores / número de valores
Mediana = valor en la mitad del conjunto de datos
Moda = valor que aparece más frecuentemente
Hay también otras fórmulas para calcular estas medidas, como la media ponderada y la mediana ponderada, pero son menos comunes.
Esperamos que este post os haya resultado útil e interesante. ¡Hasta la próxima!




 Moda y Estilo Las mejores ideas de Estilo de moda
Moda y Estilo Las mejores ideas de Estilo de moda


