¡Hola a todos! Hoy les presentamos un artículo sobre las medidas de tendencia central, algo muy importante en el mundo de la estadística. Pero no se preocupen, no necesitan ser expertos en matemáticas para entenderlo. ¡Continúen leyendo!
Table of Contents
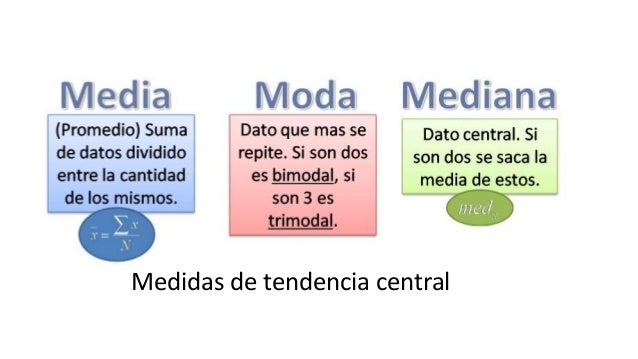
Medidas de tendencia central
Comencemos por explicar qué son las medidas de tendencia central. Básicamente, son valores que representan el centro de un conjunto de datos. Los tres más usados son la media, mediana y moda.
La media
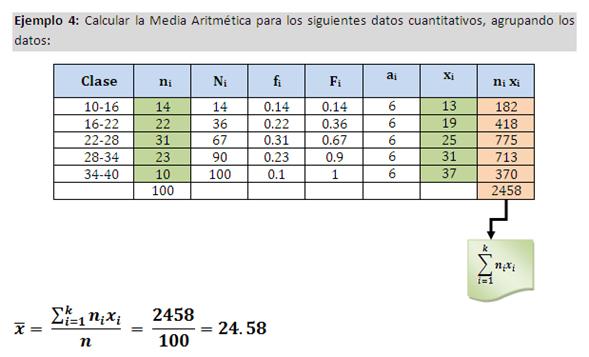
La media es el valor obtenido de sumar todos los datos y dividirlos entre el número de observaciones. Para entenderlo mejor, podemos utilizar el siguiente ejemplo:
Supongamos que queremos calcular la media de la edad de un grupo de 5 personas. Las edades son: 20, 23, 35, 40 y 55. Para calcular la media, debemos sumar todas las edades y dividirlas entre el número de personas (5). Entonces:
20 + 23 + 35 + 40 + 55 = 173
173 ÷ 5 = 34.6
Por lo tanto, la media de edad de este grupo es de 34.6 años.
La mediana
La mediana es el valor que se encuentra en la mitad de un conjunto de datos, es decir, el valor que divide la serie en dos partes iguales. Para encontrar la mediana, debemos ordenar los datos de menor a mayor y buscar el valor que se encuentra exactamente en la mitad de la serie. Si la serie tiene un número par de datos, se debe calcular la media de los dos valores centrales.
Supongamos que tenemos la siguiente serie de números:
3, 5, 7, 8, 9
Para encontrar la mediana, debemos ordenarlos de menor a mayor:
3, 5, 7, 8, 9
Como la serie tiene un número impar de datos, la mediana es el valor central, que en este caso es 7.
La moda
La moda es simplemente el valor que aparece con mayor frecuencia en la serie de datos. En algunos casos, puede no haber una moda clara o puede haber varias.

Por ejemplo, si tenemos la serie de números:
2, 4, 6, 6, 8, 8, 8, 10
La moda es el número 8, ya que aparece tres veces, mientras que los demás números aparecen solo una o dos veces.
Consejos para calcular las medidas de tendencia central
La media, mediana y moda pueden ser muy útiles para resumir un conjunto de datos, pero es importante tener en cuenta que no siempre son representativos. Por ejemplo, en una serie de números muy dispersos, la media puede ser muy diferente de la mediana, mientras que en una serie de números con muchas repeticiones, la moda puede no ser muy informativa.
Por lo tanto, es importante utilizar las tres medidas de forma conjunta para tener una idea más completa del conjunto de datos. Además, es importante tener en cuenta el objetivo del análisis, ya que en algunos casos puede ser más importante enfocarse en la mediana que en la media, por ejemplo.
Ideas para utilizar las medidas de tendencia central
Las medidas de tendencia central son muy comunes en el mundo de los negocios y la economía, ya que pueden ayudar a entender mejor los datos financieros y económicos. Por ejemplo, la media salarial de una empresa puede ser útil para decidir los salarios de los nuevos empleados o para establecer una estrategia de marketing basada en los ingresos de los clientes.

Además, las medidas de tendencia central también se utilizan en el mundo de la salud y la medicina, por ejemplo, para calcular la edad o el peso promedio de un grupo de pacientes.
Cómo calcular las medidas de tendencia central en Excel
Si bien se pueden calcular las medidas de tendencia central a mano, es mucho más fácil y preciso utilizar Excel. A continuación, les explicamos cómo hacerlo:
1. Introduzca los datos en una hoja de cálculo de Excel.
2. Seleccione la celda donde desea que aparezca la media y escriba la siguiente fórmula: =PROMEDIO(rango de celdas).
3. Seleccione la celda donde desea que aparezca la mediana y escriba la siguiente fórmula: =MEDIANA(rango de celdas).
4. Seleccione la celda donde desea que aparezca la moda y escriba la siguiente fórmula: =MODA(rango de celdas).

Conclusiones
Las medidas de tendencia central son muy útiles y se utilizan en una gran variedad de ámbitos, desde la economía y los negocios hasta la salud y la medicina. Como hemos visto, la media, mediana y moda nos permiten obtener un resumen de los datos y entender mejor su distribución.
Es importante recordar que estas medidas no son la única forma de analizar los datos y que deben utilizarse en conjunto con otras herramientas de análisis. Además, es importante tener en cuenta el objetivo del análisis y cómo se puede utilizar la información obtenida.
Esperamos que este artículo les haya sido útil. ¡Nos vemos pronto!
Referencias
Calaméo – Medidas de Tendencia Central. (s.f.). Recuperado 18 de noviembre de 2021, de https://www.calameo.com/books/101101000430-f8b90a5337a664239d462
Medidas de tendencia central. (s.f.). Recuperado 18 de noviembre de 2021, de https://www.monografias.com/docs110/media-medidas-tendencia-central-mtc/media-medidas-tendencia-central-mtc.shtml
Medidas de tendencia central. (s.f.). Recuperado 18 de noviembre de 2021, de https://es.slideshare.net/marcos_ayala27/medidas-de-tendencia-central-calculoamano
Profesor Julio Cesar Sandino: medidas de tendencia central para datos. (s.f.). Recuperado 18 de noviembre de 2021, de http://juliocesarsandino.blogspot.com/2016/01/medidas-de-tendencia-central-para-datos.html
MEDIDAS DE TENDENCIA CENTRAL MEDIA, MEDIANA, y MODA. (s.f.). Recuperado 18 de noviembre de 2021, de https://www.youtube.com/watch?v=SLFRKHVhKdI
Medidas de tendencia central. (s.f.). Recuperado 18 de noviembre de 2021, de https://www.youtube.com/watch?v=K3qBFEmtIZY
 Moda y Estilo Las mejores ideas de Estilo de moda
Moda y Estilo Las mejores ideas de Estilo de moda


