Ejemplos De Moda De Tendencia Central

Si estás estudiando matemáticas o estadísticas, seguramente has escuchado hablar de las medidas de tendencia central. Se trata de un conjunto de herramientas que nos permiten entender cómo se distribuyen los datos de una muestra o población.

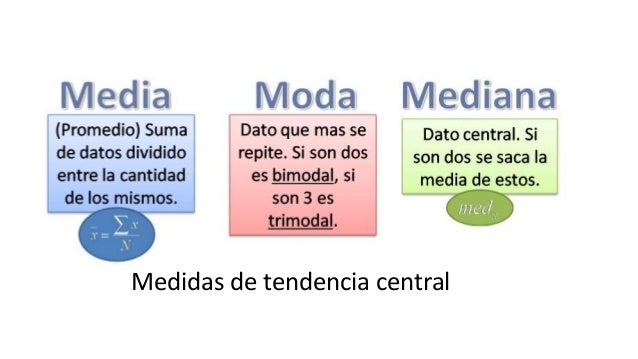
Medidas de tendencia central

La primera medida de tendencia central que debes conocer es la media aritmética, también llamada promedio. Se trata de calcular la suma de todos los valores de una muestra y luego dividirla entre el número total de elementos. Por ejemplo, si tenemos los siguientes valores: 10, 20, 30, 40, 50, la media sería (10 + 20 + 30 + 40 + 50) / 5 = 30.

Otra medida de tendencia central muy utilizada es la mediana, que consiste en ordenar los valores de menor a mayor y escoger el valor que ocupa la posición central. Si la muestra tiene un número par de elementos, se calcula la media de los dos valores centrales. Por ejemplo, en la muestra anterior (10, 20, 30, 40, 50), la mediana sería 30.

Consejos para utilizar las medidas de tendencia central

Algunos consejos para utilizar correctamente las medidas de tendencia central son:

• Verificar que los datos de la muestra no tienen valores extremos que puedan afectar el cálculo de la media
• Combinar las diferentes medidas de tendencia central para obtener una imagen más completa de los datos
• Utilizar las medidas de tendencia central junto con otras herramientas estadísticas, como los gráficos, para visualizar mejor la información

Moda

Otra medida de tendencia central es la moda, que es el valor que aparece con mayor frecuencia en una muestra. Por ejemplo, si en una muestra de 10 valores, el valor 5 aparece 4 veces y los otros valores aparecen una sola vez, entonces la moda sería 5.

Cómo utilizar las medidas de tendencia central en la vida real

Aunque las medidas de tendencia central se suelen enseñar en el ámbito académico, también son muy útiles en la vida real. Por ejemplo, si trabajas en una empresa y quieres saber cuál es el salario promedio de los empleados, puedes calcular la media aritmética. Si quieres saber cuál es el sueldo que cobra la mayoría de los empleados, puedes calcular la moda.

Por otro lado, si eres dueño de un pequeño negocio y quieres saber cuál es el producto más vendido, puedes calcular la mediana. De esta forma, sabrás cuál es el producto que se vende más frecuentemente, sin importar si algunos clientes compran grandes cantidades o si otros compran pequeñas cantidades.

Ideas para utilizar las medidas de tendencia central en el aula

Si eres profesor de matemáticas o estadística, puedes utilizar las medidas de tendencia central para enseñar a tus estudiantes cómo se analizan los datos. Algunas ideas para utilizar las medidas de tendencia central en el aula son:

• Pedir a los estudiantes que recojan datos sobre un tema de su interés y utilicen las diferentes medidas de tendencia central para analizarlos
• Motivar a los estudiantes para que piensen en situaciones reales en las que se puedan emplear las medidas de tendencia central
• Hacer que los estudiantes analicen diferentes gráficos y luegoutilicen las medidas de tendencia central para interpretarlos

Como elegir la medida de tendencia central adecuada

Para elegir la medida de tendencia central adecuada, es necesario considerar el tipo de datos que se están analizando, ya que cada medida es más apropiada para determinados tipos de datos. Por ejemplo, la media aritmética es más adecuada para datos que siguen una distribución normal, mientras que la mediana es más adecuada para datos que tienen valores extremos o que no siguen una distribución normal.

Otro factor a considerar es el tamaño de la muestra. Si la muestra es pequeña, la mediana puede ser una mejor opción que la media aritmética, ya que esta última puede verse afectada por los valores extremos. Por otro lado, si la muestra es grande, la media aritmética suele ser más estable y confiable que la mediana.

Conclusiones

Las medidas de tendencia central son una herramienta fundamental para el análisis de datos, tanto en el ámbito académico como en la vida real. Cada medida tiene sus ventajas y desventajas, por lo que es importante elegir la medida adecuada en cada situación. Si se utilizan correctamente, estas medidas nos permiten entender cómo se distribuyen los datos y tomar decisiones más informadas.