La Tendencia Central Moda Media Aritmética Y Rango

Buenas mi gente, hoy les quiero hablar sobre las medidas estadísticas de tendencia central. La media, la mediana, la moda y el rango son herramientas muy importantes en el mundo de la estadística. Aquí les voy a mostrar algunas imágenes y explicar un poquito sobre cada una de ellas.

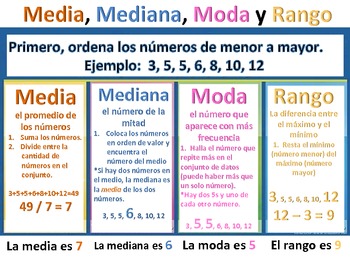
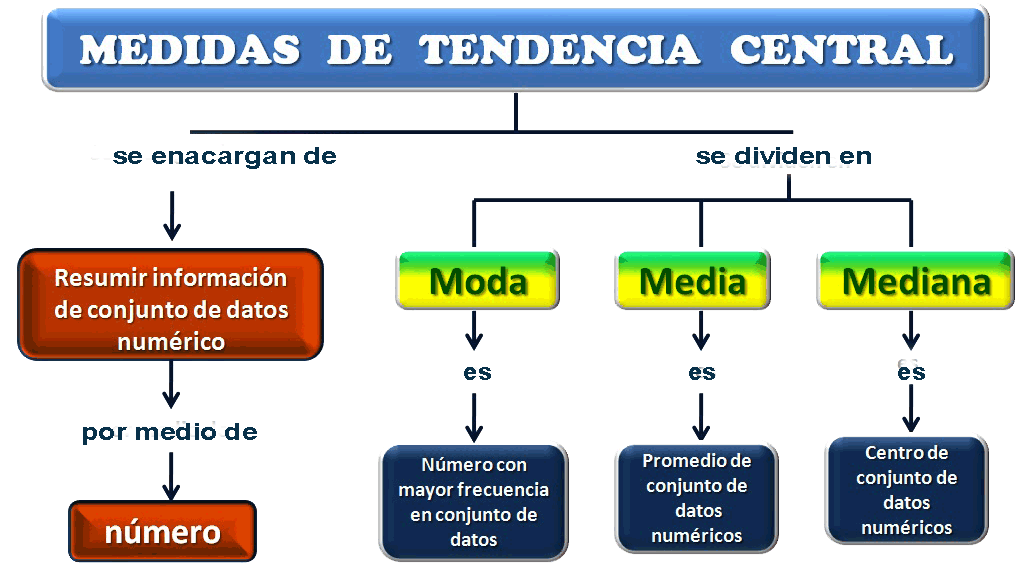
Media Aritmética

La media aritmética, también conocida como promedio, es la suma de todos los datos dividida por la cantidad de datos. Por ejemplo, si tenemos los siguientes números: 2, 4, 6, 8, 10, la media aritmética sería:

(2 + 4 + 6 + 8 + 10) / 5 = 6

La media aritmética es un buen indicador de la tendencia central de un conjunto de datos cuando no hay valores extremos. Sin embargo, si hay valores atípicos (outliers), la media aritmética puede ser engañosa. Por eso es importante analizar también la mediana y la moda.

Mediana

La mediana es el valor que ocupa la posición central de todos los datos ordenados de menor a mayor o de mayor a menor. Por ejemplo, si tenemos los siguientes números: 2, 4, 6, 8, 10, la mediana sería:

Mediana = 6

La mediana es útil cuando hay valores extremos que pueden distorsionar la media aritmética. Además, la mediana es una medida robusta, lo que significa que no se ve afectada por valores atípicos. Por eso, en algunos casos, la mediana es preferible sobre la media aritmética.

Moda

La moda es el valor que se repite con más frecuencia en un conjunto de datos. Por ejemplo, si tenemos los siguientes números: 2, 4, 6, 8, 8, 10, la moda sería 8, porque es el número que aparece dos veces, mientras que los demás aparecen solo una vez. Si todos los números aparecen la misma cantidad de veces, entonces no hay moda.

La moda es útil para identificar patrones o tendencias en un conjunto de datos, pero no siempre es una buena medida de tendencia central. Por ejemplo, si tenemos los siguientes números: 2, 4, 6, 8, 8, 10, la media aritmética sería 6, mientras que la moda sería 8. En este caso, la media aritmética es una mejor medida de tendencia central que la moda.

Rango

El rango es la diferencia entre el valor más alto y el valor más bajo en un conjunto de datos. Por ejemplo, si tenemos los siguientes números: 2, 4, 6, 8, 10, el rango sería:

Rango = 10 – 2 = 8

El rango es una medida sencilla que indica la dispersión de los datos. Sin embargo, no es una buena medida de tendencia central, ya que puede ser afectada por valores atípicos.

Consejos

• Analiza los datos antes de calcular las medidas de tendencia central.
• Usa la media aritmética cuando no hay valores extremos.
• Usa la mediana cuando hay valores extremos.
• Usa la moda para identificar patrones o tendencias en los datos, pero no siempre es una buena medida de tendencia central.
• No te olvides de tomar en cuenta el rango para tener una idea de la dispersión de los datos.

Ideas

Estas medidas son muy útiles en la estadística, pero también se pueden aplicar en muchos otros campos. Por ejemplo, en la industria pueden ser usadas para medir la calidad de un producto. En finanzas pueden ser usadas para analizar el rendimiento de una inversión. En negocios pueden ser usadas para analizar las ventas de un producto en un periodo de tiempo. La estadística es una herramienta muy poderosa que se puede aplicar en muchos ámbitos.

Cómo calcular las medidas de tendencia central

Para calcular la media aritmética, simplemente sumas todos los datos y los divides entre la cantidad de datos:

Media aritmética = (dato1 + dato2 + … + daton) / n

Para calcular la mediana, primero ordenas los datos de menor a mayor o de mayor a menor y luego buscas el valor central:

• Si la cantidad de datos es impar, la mediana es el valor que ocupa la posición central.
• Si la cantidad de datos es par, la mediana es la media de los dos valores centrales.

Para calcular la moda, simplemente buscas el valor que se repite con más frecuencia.

Para calcular el rango, simplemente restas el valor más alto del valor más bajo:

Rango = valor más alto – valor más bajo

Espero que esta información les haya sido útil. Si tienen alguna pregunta o comentario, por favor déjenlo en la sección de comentarios. ¡Hasta la próxima!