
¿Sabes qué son las medidas de tendencia central? Seguramente has escuchado hablar de ellas, pero ¿realmente sabes de qué se trata? En este artículo, te explicaremos todo lo que necesitas saber sobre este tema, con ejemplos y ejercicios para que puedas comprenderlo de forma más sencilla.
Table of Contents
¿Qué son las medidas de tendencia central?
Las medidas de tendencia central son un conjunto de estadísticas descriptivas que se utilizan para conocer la distribución de un conjunto de datos. Su objetivo es encontrar un valor que represente a las observaciones del conjunto de datos de forma adecuada.
Las tres medidas de tendencia central más utilizadas son: la media, la mediana y la moda.
La media
La media es la suma de todos los valores del conjunto de datos dividida entre el número de elementos que hay en el conjunto.
Por ejemplo, si tenemos el siguiente conjunto de datos: 1, 2, 3, 4, 5, la media se calcula de la siguiente manera:
Media = (1 + 2 + 3 + 4 + 5) / 5 = 3
Es decir, la media de este conjunto de datos es 3.
La mediana
La mediana es el valor que separa a la mitad superior de la mitad inferior del conjunto de datos ordenados. Para calcular la mediana, se deben ordenar los datos de menor a mayor y buscar el valor central. Si el número de elementos es par, la mediana se calcula como la media de los dos valores centrales.
Por ejemplo, si tenemos el siguiente conjunto de datos: 1, 2, 3, 4, 5, 6, la mediana se calcula de la siguiente manera:
Ordenamos los datos: 1, 2, 3, 4, 5, 6
La mediana es 4, ya que divide al conjunto de datos en dos partes iguales: 1, 2, 3 y 4, 5, 6.
La moda
La moda es el valor que aparece con mayor frecuencia en un conjunto de datos.
Por ejemplo, si tenemos el siguiente conjunto de datos: 1, 2, 3, 3, 4, 5, 5, 5, la moda es 5, ya que es el valor que aparece con mayor frecuencia.
Consejos
Ahora que ya sabes qué son las medidas de tendencia central, es importante tener en cuenta algunos consejos a la hora de utilizarlas:
- Las medidas de tendencia central no siempre representan al conjunto de datos de forma adecuada. Deben ser utilizadas con precaución y siempre en conjunto con otras medidas estadísticas descriptivas.
- La media es muy sensible a los valores extremos, por lo que si existen valores atípicos o extremos, puede que no sea la medida más adecuada para representar al conjunto de datos.
- La mediana es menos sensible a los valores extremos que la media, por lo que puede ser una mejor opción para conjuntos de datos con valores atípicos.
- La moda puede no ser una medida adecuada para conjuntos de datos con muchas observaciones diferentes, ya que puede que no exista un valor que se repita con suficiente frecuencia.
Ideas
Ahora que sabes cómo utilizar las medidas de tendencia central de forma adecuada, aquí te dejamos algunas ideas de cómo puedes aplicarlas:
- En el ámbito de la educación, las medidas de tendencia central pueden ser utilizadas para conocer el promedio de notas en una asignatura, identificar en qué temas los estudiantes tienen más dificultades y en qué temas se destacan.
- En el ámbito empresarial, las medidas de tendencia central pueden ser utilizadas para conocer el promedio de ventas de un producto, identificar los productos más vendidos y los menos vendidos, y detectar posibles oportunidades de mejora.
- En el ámbito de la salud, las medidas de tendencia central pueden ser utilizadas para conocer el promedio de la frecuencia cardíaca de una persona, identificar los valores de presión arterial más comunes en una población y detectar posibles factores de riesgo.
Cómo utilizar las medidas de tendencia central
A continuación, te presentamos un ejemplo práctico de cómo utilizar las medidas de tendencia central. Supongamos que queremos conocer el sueldo promedio de los trabajadores de una empresa.
- Reunimos los datos de los sueldos de todos los trabajadores. Por ejemplo: 1000, 2000, 1500, 3000, 2500, 2000, 1800, 2200, 2400, 2800.
- Calculamos la media de los sueldos:
- Calculamos la mediana de los sueldos:
- Calculamos la moda de los sueldos:
Media = (1000 + 2000 + 1500 + 3000 + 2500 + 2000 + 1800 + 2200 + 2400 + 2800) / 10 = 2200
El sueldo promedio de los trabajadores de la empresa es de 2200.
Ordenamos los sueldos: 1000, 1500, 1800, 2000, 2000, 2200, 2400, 2500, 2800, 3000
La mediana es 2200, ya que divide al conjunto de datos en dos partes iguales: 1000, 1500, 1800, 2000, 2000 y 2200, 2400, 2500, 2800, 3000.
La moda es 2000, ya que es el valor que aparece con mayor frecuencia.
Como puedes ver, las medidas de tendencia central son herramientas muy útiles para analizar conjuntos de datos y obtener información relevante. No dudes en utilizarlas en tus proyectos y actividades diarias.
Consejos
Ahora que ya conoces las medidas de tendencia central, es importante que tengas en cuenta algunos consejos a la hora de utilizarlas:
- Si estás trabajando con datos no agrupados, puedes utilizar la media, la mediana y la moda para conocer la tendencia central del conjunto de datos.
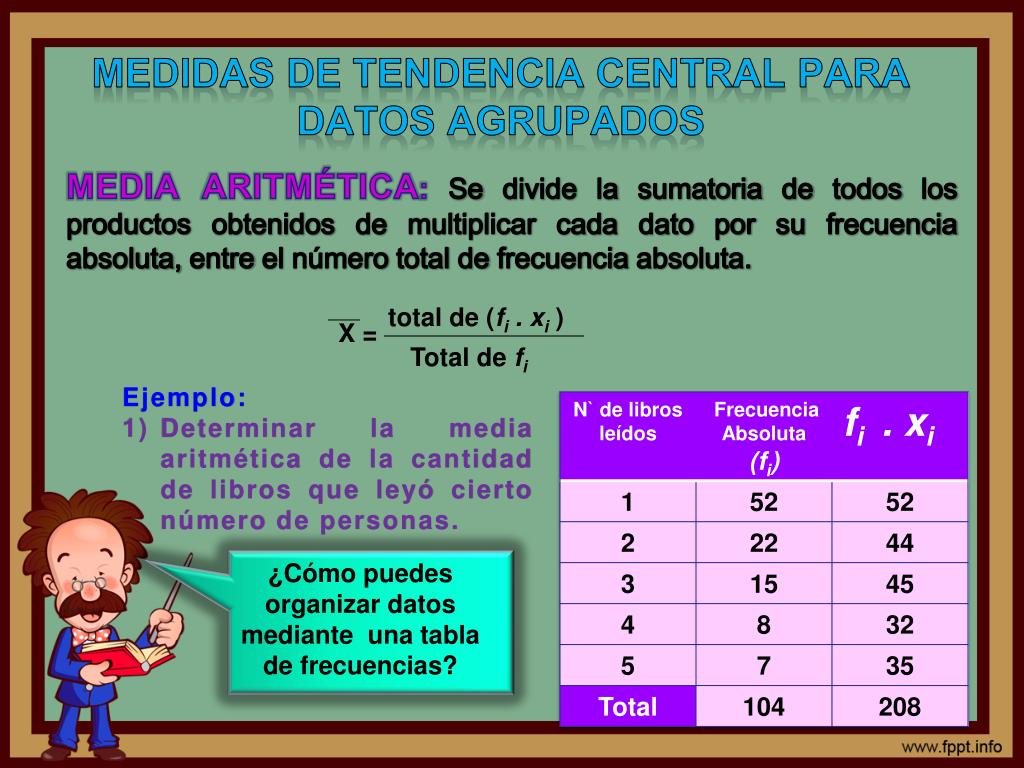
- Si estás trabajando con datos agrupados en intervalos, debes utilizar la media ponderada, la mediana y la moda ponderadas.
- Además de las medidas de tendencia central, existen otras medidas estadísticas descriptivas que pueden ser de utilidad, como la varianza, la desviación estándar y los cuartiles.
Ahora que conoces todo esto, ¡anímate a utilizar las medidas de tendencia central en tus proyectos y comienza a obtener información valiosa de tus datos!
Ideas
Aquí te dejamos algunas ideas más de cómo puedes utilizar las medidas de tendencia central:
- En el ámbito de la investigación científica, las medidas de tendencia central pueden ser utilizadas para analizar resultados de experimentos y estudios de campo.
- En el ámbito financiero, las medidas de tendencia central pueden ser utilizadas para analizar los ingresos y gastos de una empresa y detectar posibles problemas financieros.
- En el ámbito deportivo, las medidas de tendencia central pueden ser utilizadas para analizar las estadísticas de un equipo o jugador y detectar sus fortalezas y debilidades.
Cómo utilizar las medidas de tendencia central en la práctica
Para que puedas comprender de forma más clara cómo utilizar las medidas de tendencia central, a continuación te presentamos otro ejemplo práctico:
Supongamos que queremos conocer la cantidad de tiempo que pasan los estudiantes en la escuela. Para ello, realizamos una encuesta a un grupo de estudiantes de diferentes edades y niveles educativos. Estos son los resultados obtenidos:
1 hora, 2 horas, 2 horas, 3 horas, 3 horas, 3 horas, 4 horas, 5 horas, 5 horas, 6 horas, 6 horas, 6 horas, 7 horas, 8 horas, 9 horas.
- Calculamos la media de la cantidad de tiempo que pasan los estudiantes en la escuela:
- Calculamos la mediana de la cantidad de tiempo que pasan los estudiantes en la escuela:
- Calculamos la moda de la cantidad de tiempo que pasan los estudiantes en la escuela:
Media = (1 + 2 + 2 + 3 + 3 + 3 + 4 + 5 + 5 + 6 + 6 + 6 + 7 + 8 + 9) / 15 = 4.73
La media es de 4.73 horas.
Ordenamos los datos: 1, 2, 2, 3, 3, 3, 4, 5, 5, 6, 6, 6, 7, 8, 9
La mediana es 5, ya que divide al conjunto de datos en dos partes iguales: 1, 2, 2, 3, 3, 3, 4 y 5, 5, 6, 6, 6, 7, 8, 9.
La moda es 3, ya que es el valor que aparece con mayor frecuencia.
Como puedes ver, las medidas de tendencia central son de gran ayuda cuando queremos analizar conjuntos de datos y obtener información relevante de ellos. ¡No dudes en seguir utilizándolas!

En resumen, las medidas de tendencia central son una herramienta fundamental en el análisis estadístico de datos. Su correcta aplicación puede permitir obtener información valiosa para la toma de decisiones en distintos ámbitos.
Consejos
A continuación, te resumimos los consejos más importantes a tener en cuenta al utilizar las medidas de tendencia central:
- Las medidas de tendencia central deben ser utilizadas en conjunto con otras medidas estadísticas descriptivas.
- La media es sensible a los valores extremos y puede no ser la medida adecuada en algunos casos.
- La mediana es una medida menos sensible a los valores extremos que la media.
- La moda puede no ser adecuada para conjuntos de datos con muchas observaciones diferentes.
Ideas
Las medidas de tendencia central pueden ser utilizadas en la mayoría de los ámbitos en los que se manejen datos. Algunas ideas para aplicarlas son:
- En el ámbito de la salud, para conocer la frecuencia cardíaca de una población y detectar posibles factores de riesgo.
- En el ámbito financiero, para analizar los ingresos y gastos de una empresa y detectar posibles problemas financieros.
- En el ámbito educativo, para conocer el promedio de notas en una asignatura o el tiempo que los estudiantes pasan en la escuela.
Cómo utilizar las medidas de tendencia central en la práctica
Para finalizar, te presentamos un último ejemplo práctico de cómo utilizar las medidas de tendencia central:
Supongamos que queremos conocer la cantidad de dinero que los clientes de una tienda en línea gastan en un mes. Para ello, tomamos una muestra de 30 clientes y obtenemos los siguientes resultados:
50 USD, 60 USD, 70 USD, 80 USD, 90 USD, 100 USD, 110 USD, 120 USD, 130 USD, 140 USD, 150 USD, 160 USD, 170 USD, 180 USD, 190 USD, 200 USD, 210 USD, 220 USD, 230 USD, 240 USD, 250 USD, 260 USD, 270 USD, 280 USD, 290 USD, 300 USD, 310 USD, 320 USD, 330 USD, 340 USD.
- Calculamos la media de la cantidad de dinero que los clientes gastan en un mes:
- Calculamos la mediana de la cantidad de dinero que los clientes gastan en un mes:
- Calculamos la moda de la cantidad de dinero que los clientes gastan en un mes
Media = (50 + 60 + 70 + 80 + 90 + 100 + 110 + 120 + 130 + 140 + 150 + 160 + 170 + 180 + 190 + 200 + 210 + 220 + 230 + 240 + 250 + 260 + 270 + 280 + 290 + 300 + 310 + 320 + 330 + 340) / 30 = 195
La media es de 195 USD.
Ordenamos los datos: 50, 60, 70, 80, 90, 100, 110, 120, 130, 140, 150, 160, 170, 180, 190, 200, 210, 220, 230, 240, 250, 260, 270, 280, 290, 300, 310, 320, 330, 340
La mediana es 195, ya que divide al conjunto de datos en dos partes iguales: 150, 160, 170, 180, 190, 200, 210, 220, 230, 240 y 250, 260, 270, 280, 290, 300, 310, 320, 330, 340.
 Moda y Estilo Las mejores ideas de Estilo de moda
Moda y Estilo Las mejores ideas de Estilo de moda


