Media De Tendencia Central Moda

¡Hola amigos! Hoy les traigo información muy interesante sobre las medidas de tendencia central. Sabemos que las matemáticas pueden ser un poco intimidantes para algunos, pero no se preocupen, ¡vamos a explicarlo de manera simple y divertida!

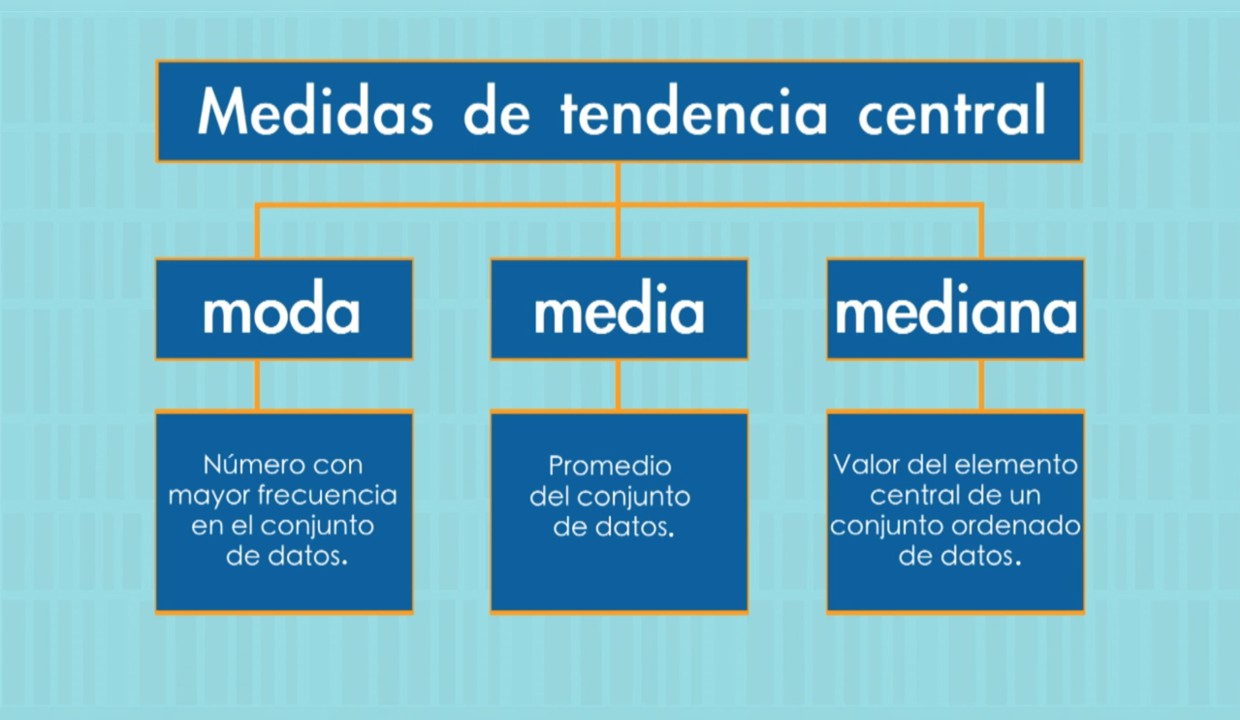
Medidas de Tendencia Central

Primero, para aquellos que quizás no estén muy familiarizados con el término, las medidas de tendencia central son un conjunto de técnicas estadísticas que nos permiten resumir y describir un conjunto de datos. Esto lo hacemos al buscar un valor que represente lo central del conjunto, es decir, una especie de promedio que nos ayude a entender mejor la información que estamos analizando.

Existen tres medidas de tendencia central principales que utilizamos comúnmente: la media, la mediana y la moda. Cada una de ellas tiene un método diferente para calcularla y puede ser útil en distintas situaciones.

Media

La media es probablemente la medida de tendencia central más conocida. Para obtenerla, sumamos todos los valores del conjunto de datos y luego los dividimos entre el número total de elementos. Es decir, supongamos que tenemos los siguientes números: 2, 4, 6, 8 y 10. Para saber cuál es la media, sumaríamos 2+4+6+8+10= 30, y luego dividiríamos entre 5 (ya que hay cinco números en el conjunto): 30/5= 6. La media en este caso es 6.

Esta medida puede ser muy útil cuando tenemos un conjunto de datos donde los valores no se diferencian mucho entre sí. Por ejemplo, si queremos conocer el promedio de edad de un grupo de personas. Sin embargo, la media puede ser muy afectada por valores extremos, también conocidos como “outliers”. En el siguiente conjunto de datos: 10, 12, 14, 16 y 75, la media sería 25.4, lo que no representa de manera precisa la información que estamos analizando.

Mediana

La mediana, por otro lado, es el valor que se encuentra en el medio de un conjunto de datos cuando lo organizamos de manera ascendente o descendente. Si volvemos a nuestro conjunto de datos anterior: 2, 4, 6, 8 y 10, la mediana sería 6, ya que es el valor que se encuentra en la mitad de la lista. Si tenemos un conjunto de datos con una cantidad par de elementos, simplemente tomamos los dos valores que están en el medio y calculamos su promedio para obtener la mediana.

La mediana es una medida menos afectada por los valores extremos, por lo que puede ser mucho más representativa de la información que estamos analizando si nuestro conjunto de datos tiene muchos “outliers”. Sin embargo, puede ser un poco complicada de calcular si tenemos un conjunto de datos muy grande.

Moda

Por último, la moda es simplemente el valor que más se repite en nuestro conjunto de datos. En nuestro conjunto original de 2, 4, 6, 8 y 10, la moda sería 0, ya que ningún valor se repite. Si tenemos un conjunto con valores repetidos, siempre habrá una moda. Por ejemplo, si nuestro conjunto de datos es 2,2,4,6,8,10, la moda sería 2.

La moda es muy útil cuando tenemos conjuntos de datos que tienen una alta frecuencia de ciertos valores. Por ejemplo, si queremos saber cuál es el color de cabello más común entre un grupo de personas, la moda podría decirnos rápidamente cuál es este valor. Sin embargo, la moda tampoco es muy representativa si tenemos valores extremos en nuestro conjunto.

Consejos

En general, es importante tener una buena comprensión de cada una de las medidas de tendencia central y saber cuál es la más adecuada para el conjunto de datos que estamos analizando. Para esto, es importante tener algunos consejos en mente:

1. No te confíes únicamente en una medida: Es importante utilizar varias medidas de tendencia central al mismo tiempo para tener una visión más completa y más representativa de la información que estamos analizando. Si solamente utilizamos la media, por ejemplo, podríamos estar ignorando información valiosa en nuestro conjunto de datos.

2. Ten en cuenta los valores extremos: Si nuestro conjunto de datos tiene puntos extremos muy altos o muy bajos, puede ser necesario utilizar medidas de tendencia central que no se vean afectadas por ellos. En este caso, la mediana y la moda pueden ser más útiles que la media.

Ideas

Una vez que comprendemos las medidas de tendencia central, podemos utilizarlas en muchos aspectos de nuestra vida diaria. Aquí hay algunas ideas:

1. Negocios: Si estamos llevando a cabo un análisis de ventas o marketing, las medidas de tendencia central pueden ayudarnos a comprender mejor qué productos o servicios son los más populares. También nos permiten analizar el ingreso de nuestra compañía y compararlo con las ventas de la competencia.

2. Investigación: Utilizar medidas de tendencia central es muy común en investigaciones científicas para analizar datos. Por ejemplo, podemos utilizarlas para encontrar el promedio de edad o peso de una población, o para analizar los resultados de un experimento.

3. Educación: Las medidas de tendencia central son muy útiles en la educación para comprender mejor el rendimiento de los estudiantes. Podemos utilizarlas para analizar los resultados de un examen y determinar las áreas en las que los estudiantes necesitan más ayuda.

Cómo utilizar las medidas de tendencia central

En resumen, las medidas de tendencia central son herramientas muy útiles para analizar conjuntos de datos. Son fáciles de calcular y pueden ofrecernos información valiosa sobre cualquier situación que estamos analizando.

Pueden ser utilizadas en cualquier aspecto de nuestras vidas, desde los negocios hasta la educación. Lo importante es tener una buena comprensión de las tres medidas principales: la media, la mediana y la moda, y saber cuál es la más adecuada para el conjunto de datos que estamos analizando.

¡Así que no teman a las matemáticas! Aprendiendo sobre las medidas de tendencia central podemos comprender mejor el mundo que nos rodea y tomar mejores decisiones.

Conclusión

En conclusión, las medidas de tendencia central son una herramienta muy valiosa en el análisis de datos. Nos permiten resumir y describir conjuntos de datos, y pueden ser utilizadas en cualquier aspecto de nuestras vidas, desde los negocios hasta la educación.

Es importante tener una buena comprensión de las tres medidas principales: la media, la mediana y la moda, y saber cuál es la más adecuada para el conjunto de datos que estamos analizando. ¡Así que no tengan miedo de las matemáticas y sigan aprendiendo!

¡Gracias por leer!