Media Mediana Moda Y Tendencia

¡Hola a todos! En este post les traigo información sobre la media, la mediana y la moda, que son medidas de tendencia central muy importantes en matemáticas. Además, les mostraré algunos ejemplos y consejos útiles para entender cómo utilizarlas adecuadamente.

Pelearse a fondo empleo media mediana y moda primaria pavimento

La media, también conocida como promedio, es la suma de todos los valores de un conjunto de datos dividida entre el número de elementos que hay en ese conjunto. Para encontrar la media, simplemente se suman todos los valores y se dividen entre la cantidad de datos.

La mediana es el valor que separa un conjunto de datos en dos partes iguales. Para encontrar la mediana, primero se ordenan los datos de menor a mayor o de mayor a menor, dependiendo de cuál sea el caso. Luego, se ubica el valor que está en el medio de la lista. Si hay un número par de datos, se promedian los dos valores que están en el centro.

View Media Moda E Mediana Ferretto Tips – Lete

La moda es el valor que se repite con mayor frecuencia en un conjunto de datos. Es decir, es el valor que aparece más veces. En algunos casos, un conjunto de datos puede no tener moda, o puede tener varias modas si hay varios valores que se repiten con la misma frecuencia.

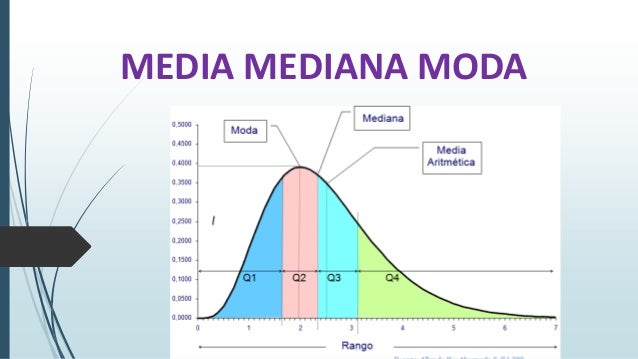
Ahora bien, ¿para qué sirven estas medidas de tendencia central? Pues, en términos generales, nos permiten resumir de manera general las características de un conjunto de datos. Además, son muy útiles para hacer comparaciones entre diferentes conjuntos de datos y para ver cómo se distribuyen los valores dentro de un conjunto.

Media, mediana, moda y rango – YouTube

Para entender mejor cómo funcionan estas medidas, les mostraré algunos ejemplos. Supongamos que queremos conocer el salario promedio de un grupo de 10 personas. Estos son los salarios de cada uno:

• 1000
• 1200
• 800
• 1500
• 1100
• 1000
• 900
• 1300
• 1200
• 1400

Para encontrar la media, simplemente sumamos todos los valores y los dividimos entre la cantidad de datos:

Media = (1000 + 1200 + 800 + 1500 + 1100 + 1000 + 900 + 1300 + 1200 + 1400) / 10 = 1180

Por lo tanto, el salario promedio de este grupo de 10 personas es de 1180 dólares. Ahora, veamos cómo encontrar la mediana. Primero, ordenamos los salarios de menor a mayor:

• 800
• 900
• 1000
• 1000
• 1100
• 1200
• 1200
• 1300
• 1400
• 1500

Como hay un número par de datos, tomamos los dos valores que están en el centro y los promediamos:

Mediana = (1100 + 1200) / 2 = 1150

La mediana de este grupo de personas es de 1150 dólares. Finalmente, para encontrar la moda, simplemente contamos cuántas veces aparece cada valor:

• 800: 1 vez
• 900: 1 vez
• 1000: 2 veces
• 1100: 1 vez
• 1200: 2 veces
• 1300: 1 vez
• 1400: 1 vez
• 1500: 1 vez

Como podemos ver, el valor que más veces aparece es 1000, por lo que la moda de este conjunto de datos es de 1000 dólares.

Qué es la moda en matemáticas y cómo se obtiene – Conocimientos Generales

Por supuesto, estos son solo ejemplos simples. En la vida real, los conjuntos de datos pueden ser mucho más grandes y complejos, por lo que encontrar la media, la mediana y la moda puede ser un poco más complicado. Sin embargo, con un poco de práctica, todo se vuelve más fácil.

Algunas ideas útiles que les pueden servir a la hora de trabajar con estas medidas de tendencia central son:

• Si el conjunto de datos es muy grande, es recomendable utilizar una calculadora para ahorrar tiempo y evitar errores.
• Es importante ordenar los datos antes de buscar la mediana.
• A la hora de buscar la moda, es conveniente hacer una tabla con los valores y su frecuencia para tener una mejor visualización.
• Siempre es importante considerar el contexto en el que se está trabajando para interpretar adecuadamente las medidas de tendencia central.

Florero Jardines Precaución Tendencia Central Media Mediana Y Moda

Finalmente, les dejaré algunos ejercicios para que practiquen y sigan mejorando sus habilidades con la media, la mediana y la moda:

1. En un curso de 30 alumnos, las notas más altas fueron 10 y las más bajas fueron 2. Si la nota promedio del curso es de 7.5, ¿cuál es la mediana?

2. En un grupo de amigos, los siguientes son los pesos en kilogramos: 75, 80, 60, 70, 68. ¿Cuál es la moda?

3. En una prueba de selección de personal, los datos de edad de los candidatos son los siguientes: 23, 45, 32, 21, 45, 36, 29, 24, 27, 30. ¿Cuál es la media?

Espero que este post les haya sido útil y que ahora se sientan más seguros a la hora de trabajar con la media, la mediana y la moda en matemáticas. ¡Recuerden siempre practicar para seguir mejorando!