La estadística es una materia interesante para aquellos que disfrutan de los números y el análisis de datos. Una de las herramientas más importantes en estadística son las medidas de tendencia central, las cuales nos permiten saber cuál es el valor central de un conjunto de datos. En este artículo veremos algunos consejos e ideas para comprender las medidas de tendencia central de manera más sencilla.
Table of Contents
Las medidas de tendencia central
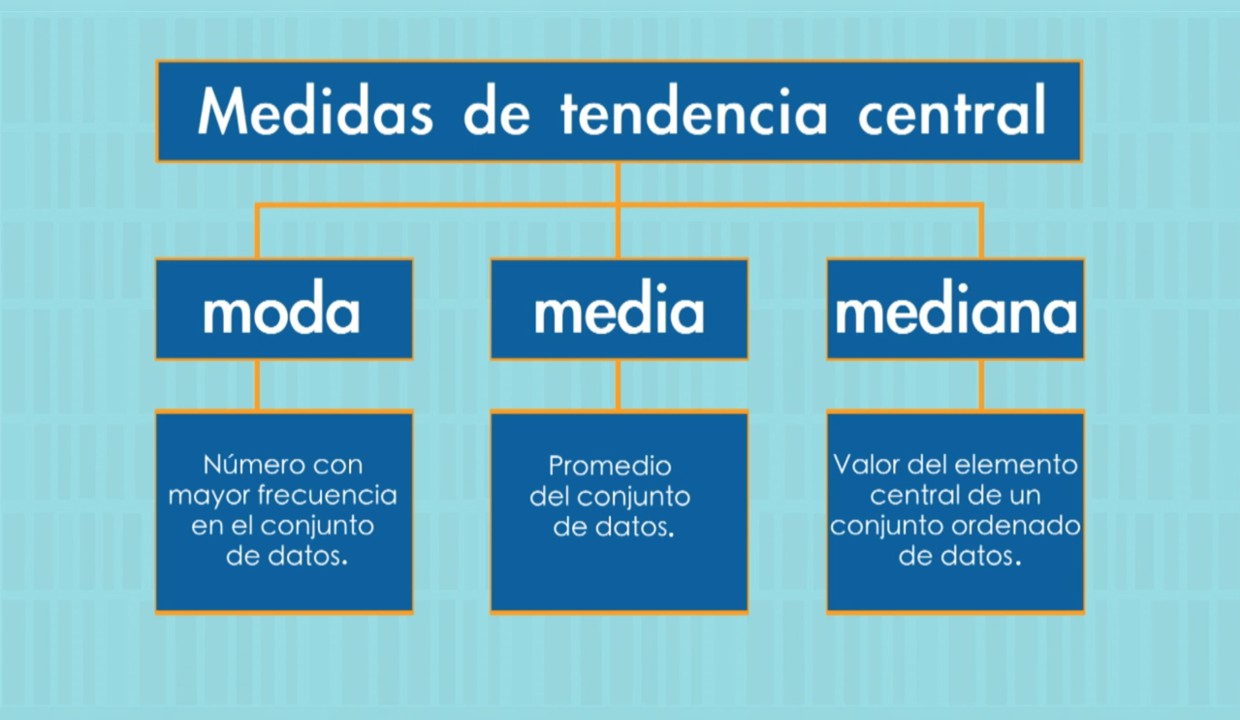
Las medidas de tendencia central son herramientas que se utilizan en estadística para describir la posición central de un conjunto de datos. Las tres medidas de tendencia central más comunes son la media, la mediana y la moda.
La media
La media es la medida de tendencia central más comúnmente utilizada. Se calcula sumando todos los valores del conjunto de datos y luego dividiendo la suma total entre el número de elementos en el conjunto de datos. La media puede ser influenciada en gran medida por valores extremos o atípicos, lo que puede hacer que no sea una medida representativa de los datos.
Algunas consejos para trabajar con la media es que esta puede ser utilizada para comparar dos o más conjuntos de datos. Por ejemplo, si queremos saber cuál es el promedio salarial de los trabajadores de distintas empresas, podemos utilizar la media para hacer la comparación. La media también es útil para identificar valores extremos o atípicos en un conjunto de datos, pues estos pueden afectar significativamente su valor.
La mediana
La mediana es la medida de tendencia central que se encuentra en la posición intermedia de un conjunto de datos ordenado. Para calcular la mediana, es necesario ordenar los datos de menor a mayor y encontrar el valor que se encuentra en la posición central. Si el conjunto de datos es impar, entonces la mediana será el valor que se encuentra en la posición central exacta. Si el conjunto de datos es par, entonces se suman los valores que se encuentran en las dos posiciones centrales y se divide el resultado entre dos.

La mediana es una medida de tendencia central más robusta que la media, ya que no es afectada por valores extremos o atípicos. Esto hace que la mediana sea una medida más representativa de los datos en general. Sin embargo, la mediana puede no ser tan fácil de interpretar como la media, pues no es una medida muy comúnmente utilizada fuera del campo de la estadística.
La moda
La moda es la medida de tendencia central que representa el valor que aparece con mayor frecuencia en un conjunto de datos. La moda no siempre es fácil de encontrar, especialmente si el conjunto de datos es muy grande o si no hay un valor que se repita con mucha frecuencia. Además, es importante mencionar que un conjunto de datos puede tener más de una moda.

Una de las principales aplicaciones de la moda es en el análisis de distribuciones. Si una distribución es simétrica, entonces la moda, la mediana y la media tendrán valores similares. Si la distribución es asimétrica, entonces estos tres valores pueden presentar diferencias significativas. En general, la moda no es tan utilizada como la media o la mediana, pero puede ser útil en algunos análisis específicos.
Consejos sobre las medidas de tendencia central
Estas son algunas consejos que pueden ayudar a comprender mejor las medidas de tendencia central:
- Es importante recordar que las medidas de tendencia central no siempre son representativas de los datos en su totalidad. Es posible que un conjunto de datos tenga valores atípicos o que no siga una distribución normal, lo que puede afectar significativamente las medidas de tendencia central.
- Es importante utilizar las medidas de tendencia central adecuadas para cada conjunto de datos. Por ejemplo, si los datos tienen valores extremos, es posible que la mediana sea una medida más representativa que la media.
- Es importante tener en cuenta el tamaño del conjunto de datos al utilizar medidas de tendencia central. En general, cuanto más grande sea el conjunto de datos, más representativas serán las medidas de tendencia central.
- Es importante analizar las medidas de tendencia central en conjunto con otras medidas estadísticas, como la desviación estándar o el rango intercuartílico, para tener una mejor comprensión de los datos en su totalidad.
Ideas para trabajar con medidas de tendencia central
Estas son algunas ideas para trabajar con medidas de tendencia central en distintos contextos:
- En el contexto de los negocios, se pueden utilizar medidas de tendencia central para comparar el rendimiento de distintas empresas. Por ejemplo, es posible comparar el promedio de ventas de distintas empresas o el promedio de días que tardan en cobrar por sus productos o servicios.
- En el contexto de la educación, se pueden utilizar medidas de tendencia central para analizar el desempeño de los estudiantes en distintas asignaturas. Por ejemplo, es posible comparar el promedio de calificaciones de distintos grupos de estudiantes o el promedio de calificaciones de los estudiantes en una misma asignatura a lo largo del tiempo.
- En el contexto de la salud, se pueden utilizar medidas de tendencia central para analizar ciertas características de una población. Por ejemplo, es posible analizar el promedio de edad de los pacientes en un hospital o el promedio de niveles de glucosa en sangre en una población diabética.
Cómo trabajar con medidas de tendencia central
Estos son algunos consejos para trabajar con medidas de tendencia central:
- Es importante tener claridad con respecto a los datos que se van a analizar y las medidas de tendencia central que se van a utilizar.
- Es importante utilizar software estadístico adecuado para el análisis de los datos, como Excel o SPSS.
- Es importante tener precaución al interpretar las medidas de tendencia central, pues estas pueden verse afectadas por valores extremos o por una distribución no normal de los datos.
En resumen, las medidas de tendencia central son herramientas esenciales en estadística que nos permiten describir la posición central de un conjunto de datos. Si bien las medidas de tendencia central pueden ser afectadas por valores extremos o por una distribución no normal de los datos, estas siguen siendo una herramienta muy útil para el análisis de datos en distintos contextos.
 Moda y Estilo Las mejores ideas de Estilo de moda
Moda y Estilo Las mejores ideas de Estilo de moda


