
¡Hola amigos! ¿Cómo están hoy? Hoy vamos a hablar de un tema muy interesante: las medidas estadísticas univariantes. ¿Qué es eso? Bueno, en esencia son medidas que nos indican cómo está distribuida una variable. Y hay varias medidas que podemos usar para hacer esto.
Table of Contents
Medidas de tendencia central
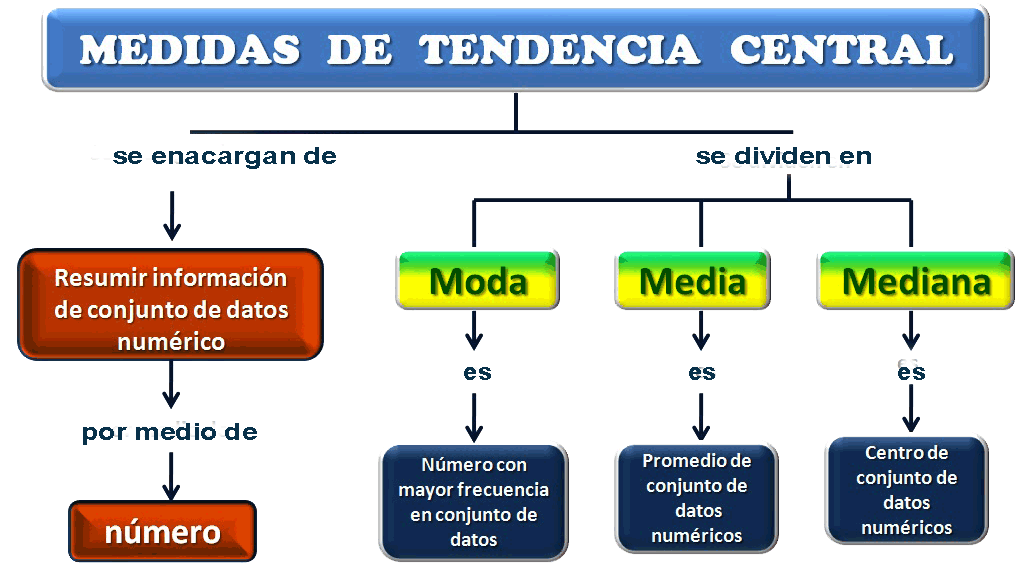
Empecemos hablando de las medidas de tendencia central. Estas medidas nos indican dónde se concentran los datos. Las tres medidas de tendencia central que más se usan son la media, la mediana y la moda.
Media
La media es el valor promedio de los datos. Para calcularla, simplemente sumamos todos los datos y los dividimos entre el número de datos. Por ejemplo, si tenemos los datos 2, 4, 6 y 8, la media sería:
(2 + 4 + 6 + 8) / 4 = 5
Así que la media de estos datos es 5.
Mediana
La mediana es el valor que está en el centro de los datos cuando los ordenamos. Por ejemplo, si tenemos los datos 2, 4, 6 y 8, los ordenamos de menor a mayor:
2, 4, 6, 8
El valor que está en el centro de estos datos es 6, así que la mediana es 6.
Moda
La moda es el valor que se repite más veces en los datos. Por ejemplo, si tenemos los datos 2, 4, 6, 6 y 8, la moda es 6 porque es el valor que se repite dos veces.

Medidas de dispersión
Ahora hablemos de las medidas de dispersión. Estas medidas nos indican cuánto se dispersan los datos. Las dos medidas de dispersión que más se usan son el rango y la desviación estándar.
Rango
El rango es la diferencia entre el valor máximo y el valor mínimo de los datos. Por ejemplo, si tenemos los datos 2, 4, 6 y 8, el valor máximo es 8 y el valor mínimo es 2, así que el rango es:
8 – 2 = 6
Así que el rango de estos datos es 6.
Desviación estándar
La desviación estándar nos indica cuánto se alejan los datos de la media. Es una medida de dispersión más precisa que el rango, ya que tiene en cuenta todos los datos y no solo el máximo y el mínimo.
Para calcular la desviación estándar, primero calculamos la desviación de cada dato respecto a la media. La desviación de un dato es la diferencia entre ese dato y la media.
Por ejemplo, si tenemos los datos 2, 4, 6 y 8, la media es 5. La desviación del primer dato (2) es:
2 – 5 = -3
La desviación del segundo dato (4) es:
4 – 5 = -1
Y así sucesivamente hasta que hemos calculado la desviación de todos los datos.
Después, calculamos la media de estas desviaciones. Esta media es igual a cero si los datos están distribuidos de manera simétrica respecto a la media (es decir, si hay tantos datos por encima de la media como por debajo). Si los datos están más concentrados por encima o por debajo de la media, la media de las desviaciones será positiva o negativa, respectivamente.
Para obtener la desviación estándar, tomamos la raíz cuadrada de la media de las desviaciones al cuadrado (porque las desviaciones pueden ser negativas).
Es un poco complicado de explicar, así que aquí te dejo una fórmula:

Consejos para interpretar las medidas
Entonces, ¿cómo podemos interpretar estas medidas? Aquí te dejo algunos consejos.
- Si los datos están distribuidos de manera simétrica respecto a la media, la media y la mediana serán similares. Si los datos están muy concentrados alrededor de la media, la desviación estándar será pequeña.
- Si los datos están muy dispersos, el rango será grande y la desviación estándar también será grande.
- La moda puede ser útil para identificar valores atípicos o anómalos en los datos. Si el valor que se repite más veces es muy diferente del resto de los valores, puede ser un indicio de que esos valores son anómalos.
Ideas para aplicar las medidas
Las medidas de tendencia central y dispersión pueden ser útiles en muchas áreas de la vida. Aquí te dejo algunas ideas:
- En un negocio, puedes usar la media y la desviación estándar para conocer el promedio de ventas y cuánto varían estas ventas de un día a otro.
- En una encuesta, puedes usar la media y la moda para conocer las opiniones más comunes sobre un tema y cuál es la opinión media.
- En un estudio médico, puedes usar la media y la desviación estándar para conocer el promedio de una variable (como la presión arterial) en una población y cuánto varía esta variable de un individuo a otro.
Cómo calcular las medidas en Excel
Si quieres calcular estas medidas en Excel, aquí te dejo los pasos:
- Para calcular la media, usa la función AVERAGE (o PROMEDIO en español).
- Para calcular la mediana, usa la función MEDIAN.
- Para calcular la moda, usa la función MODE.SNGL.
- Para calcular el rango, resta el valor máximo menos el valor mínimo.
- Para calcular la desviación estándar, usa la función STDEV.P (para una población) o STDEV.S (para una muestra).

Conclusión
Bueno, amigos, espero que esta introducción a las medidas estadísticas univariantes les haya sido útil. Como hemos visto, estas medidas nos permiten entender mejor cómo se distribuyen los datos y sacar conclusiones útiles. Recuerda que estas medidas pueden aplicarse en muchos campos diferentes, desde los negocios hasta la medicina, así que ¡no dudes en ponerlas en práctica!

Y recuerda que si tienes alguna duda o pregunta, siempre puedes buscar más información o preguntar a un experto. ¡Aprender es divertido!
Referencias:
- https://es.wikipedia.org/wiki/Medidas_de_tendencia_central
- https://es.wikipedia.org/wiki/Medidas_de_dispersión
- https://support.microsoft.com/en-us/office/measures-of-central-tendency-mean-median-and-mode-81a824f4-ceed-bf19-819a-fcb7bd2871c2

 Moda y Estilo Las mejores ideas de Estilo de moda
Moda y Estilo Las mejores ideas de Estilo de moda


