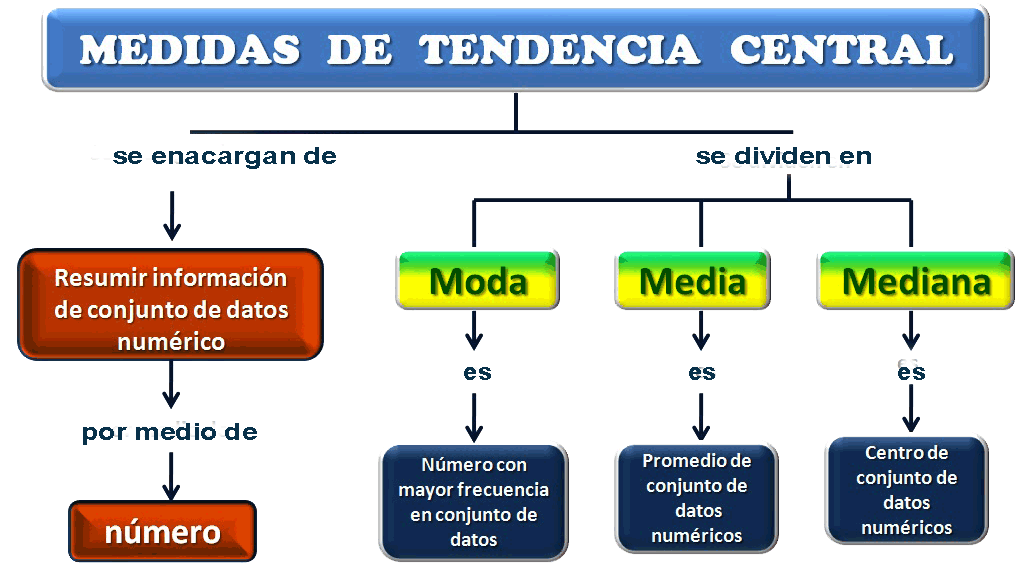
¡Hola amigos! Hoy quiero hablarles sobre un tema muy interesante: Las medidas de tendencia central. Estas medidas nos permiten conocer la posición central de un conjunto de datos y son muy importantes en el campo de la estadística. Saber cómo calcularlas y entender su significado nos ayudará a comprender mejor los datos y tomar decisiones más informadas.
Table of Contents
Media
La media, también conocida como promedio, es el resultado de sumar todos los valores de un conjunto de datos y luego dividir entre la cantidad de valores. Por ejemplo, si tenemos los siguientes valores: 2, 5, 7 y 10, la media sería:
(2+5+7+10)/4 = 6
La media nos permite conocer el valor promedio de un conjunto de datos, pero puede ser afectada por valores atípicos que se alejen mucho del resto de los valores. Por lo tanto, es recomendable utilizarla en conjunto con otras medidas de tendencia central.
Mediana
La mediana es el valor que se encuentra en el centro de un conjunto de datos ordenado. Para calcularla, se deben ordenar los valores de menor a mayor y buscar el valor que se encuentra en la posición central. En el ejemplo anterior, si ordenamos los valores de menor a mayor, quedarían así: 2, 5, 7 y 10. Como el conjunto de datos tiene un número par de valores, la mediana sería la media de los valores que se encuentran en las dos posiciones centrales.
Mediana = (5+7)/2 = 6
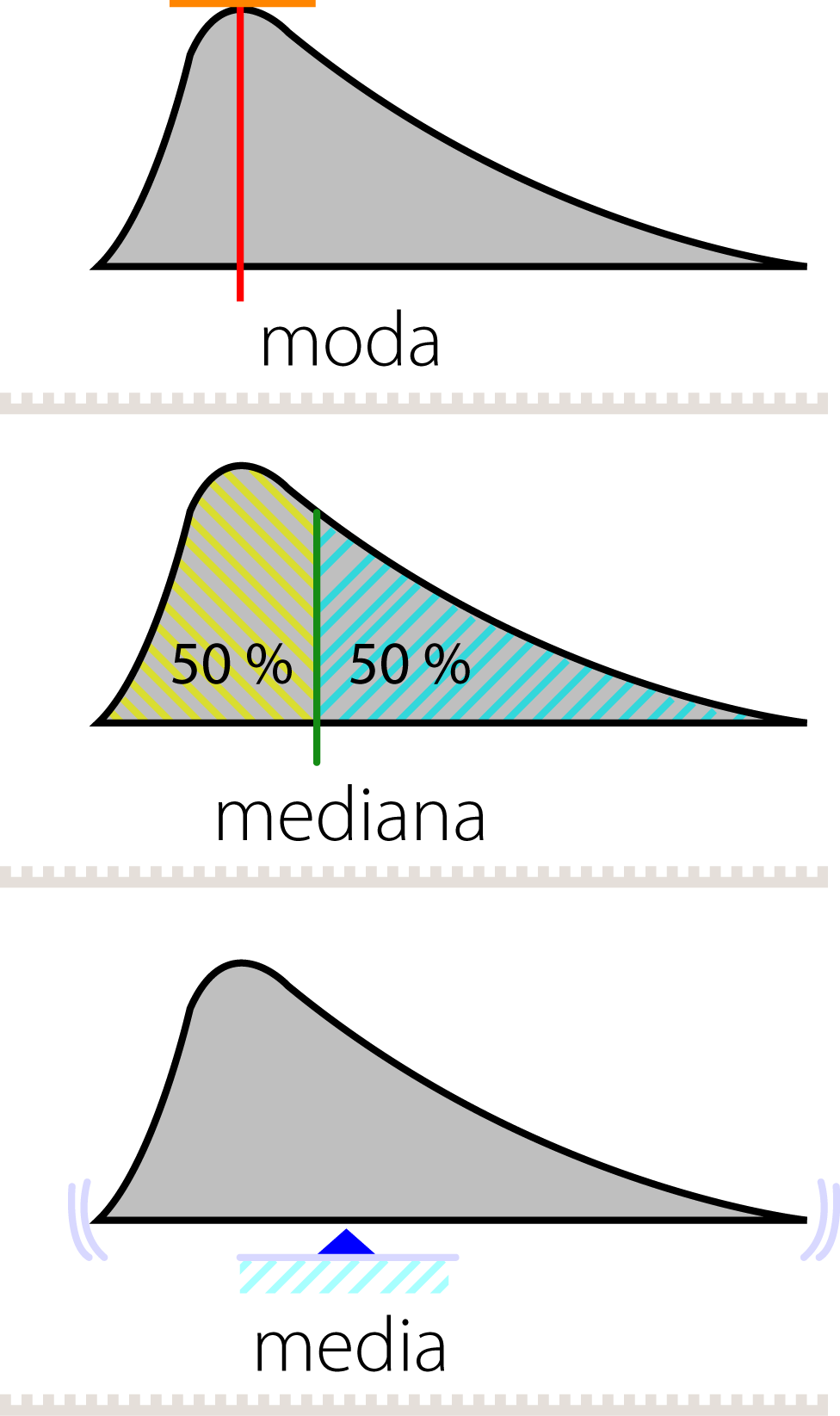
La mediana es útil porque no es afectada por valores atípicos como la media, pero no toma en cuenta todos los valores del conjunto de datos.
Moda
La moda es el valor que se repite con mayor frecuencia en un conjunto de datos. Si no hay ningún valor que se repita, entonces no hay moda. En el ejemplo anterior, la moda sería 2 porque es el valor que aparece con mayor frecuencia (una sola vez). Si tenemos valores como 2, 2, 5 y 7, entonces la moda sería 2 porque es el valor que se repite dos veces.
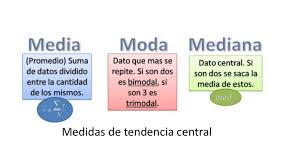
La moda es útil porque nos permite identificar los valores más comunes en un conjunto de datos, pero no nos dice nada sobre la distribución de los demás valores.
Como pueden ver, cada una de estas medidas de tendencia central nos aporta información diferente sobre un conjunto de datos. Es importante utilizarlas en conjunto y ser críticos al momento de interpretar los resultados. A continuación, les daremos algunos consejos para utilizar estas medidas de manera efectiva en su análisis de datos.
Consejos
1. Antes de utilizar las medidas de tendencia central, asegúrate de que los datos sean representativos y tengan sentido. Si tienes alguna duda, revisa los datos y vuelve a calcular las medidas.
2. Utiliza varias medidas de tendencia central para tener una imagen más completa. Es recomendable utilizar la media, la mediana y la moda de manera conjunto.
3. Ten en cuenta que las medidas de tendencia central pueden ser afectadas por valores atípicos o outliers. Si observas que hay valores que se alejan mucho del resto, es recomendable utilizar medidas más robustas como la mediana.
4. Si estás comparando conjuntos de datos, asegúrate de utilizar las mismas medidas de tendencia central en todos los casos para que los resultados sean comparables.
5. No confíes solamente en las medidas de tendencia central. Es importante analizar la distribución completa de los datos y tener en cuenta otros factores que puedan estar afectando los resultados.
Ahora que conoces más sobre las medidas de tendencia central, te daremos algunas ideas para utilizarlas en tus propios análisis de datos.
Ideas
1. Si eres maestro, puedes utilizar las medidas de tendencia central para analizar los resultados de tus estudiantes en los exámenes. De esta manera, podrás identificar qué temas necesitan más refuerzo y qué áreas se dominan bien.
2. Si eres investigador, puedes utilizar las medidas de tendencia central para analizar los resultados de tus experimentos. De esta manera, podrás identificar los resultados más relevantes y tomar decisiones informadas sobre los próximos pasos en tu investigación.
3. Si eres empresario, puedes utilizar las medidas de tendencia central para analizar tus ventas y el comportamiento de tus clientes. De esta manera, podrás identificar qué productos son los más populares y qué estrategias están funcionando mejor para atraer a tus clientes.
Como pueden ver, las medidas de tendencia central son muy útiles en diferentes campos y situaciones. Si quieres aprender más sobre ellas, te invitamos a investigar más y a utilizarlas en tus propios análisis de datos.
Cómo calcular las medidas de tendencia central
Si estás interesado en calcular las medidas de tendencia central por ti mismo, aquí te dejamos algunas fórmulas:
Media: Suma de todos los valores / Cantidad de valores
Mediana: Si el conjunto de datos tiene un número impar de valores, la mediana es el valor que se encuentra en la posición central. Si tiene un número par de valores, la mediana es la media de los valores que se encuentran en las dos posiciones centrales.
Moda: El valor que se repite con mayor frecuencia en el conjunto de datos. Si no hay ningún valor que se repita, entonces no hay moda.
Espero que esta información les haya sido útil. Recuerden que las medidas de tendencia central son una herramienta poderosa para entender los datos y tomar decisiones informadas. ¡Hasta la próxima amigos!
 Moda y Estilo Las mejores ideas de Estilo de moda
Moda y Estilo Las mejores ideas de Estilo de moda


