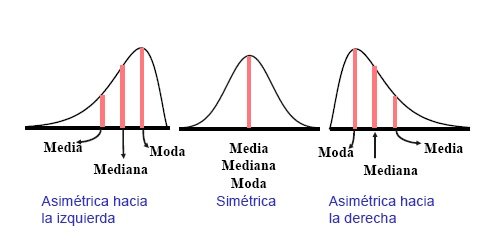
La estadística es una rama de las matemáticas que estudia la recolección, análisis e interpretación de datos. Una de las herramientas más útiles de la estadística son las medidas de tendencia central, que nos permiten resumir la información de un conjunto de datos en un solo valor representativo. En este artículo, te explicaremos en qué consisten las medidas de tendencia central y cómo se calculan.
Table of Contents
Media aritmética
La media aritmética, o simplemente “media”, es el valor obtenido al sumar todos los datos y dividir entre el número de datos. Por ejemplo, si tenemos los siguientes datos:
La media se calcularía de la siguiente manera:
Media = (10 + 15 + 20 + 25 + 30) / 5 = 20
La media aritmética tiene la ventaja de ser fácil de calcular y de interpretar, pero es sensible a los valores extremos o “outliers”. Por ejemplo, si añadiéramos un dato extremadamente alto a nuestro ejemplo anterior, como un 100:

La media aumenta significativamente:
Media = (10 + 15 + 20 + 25 + 30 + 100) / 6 = 31.67
En este caso, la media no sería un valor representativo del conjunto de datos debido al outlier.
Mediana
La mediana es el valor que divide el conjunto de datos en dos partes iguales. Para calcular la mediana, los datos deben estar ordenados de menor a mayor o de mayor a menor. Si el número de datos es impar, la mediana es el valor central. Ejemplo:
Datos: 10, 15, 20, 25, 30
Mediana = 20
Si el número de datos es par, la mediana se calcula como la media de los dos valores centrales. Ejemplo:
Datos: 10, 15, 20, 25, 30, 35
Mediana = (20 + 25) / 2 = 22.5
La mediana tiene la ventaja de ser menos sensible a los valores extremos que la media aritmética, ya que solo depende de los valores centrales del conjunto de datos. Sin embargo, puede ser difícil de calcular en conjuntos de datos muy grandes o complejos. Además, si el conjunto de datos presenta valores repetidos, la mediana puede no ser un valor existente en el conjunto.
Moda
La moda es el valor que se repite más veces en el conjunto de datos. Ejemplo:
Datos: 10, 15, 20, 25, 30, 25, 25
Moda = 25
La moda puede ser útil para identificar valores que se presentan con mayor frecuencia en el conjunto de datos. Sin embargo, puede no existir una moda en algunos conjuntos de datos o puede haber varias modas. Además, la moda no tiene en cuenta la totalidad del conjunto de datos, sino solo los valores repetidos.
Rango y eje medio
El rango es la diferencia entre el valor máximo y el valor mínimo del conjunto de datos. Ejemplo:
Datos: 10, 15, 20, 25, 30
Rango = 30 – 10 = 20
El eje medio es el promedio entre el valor máximo y el valor mínimo del conjunto de datos. Ejemplo:
Datos: 10, 15, 20, 25, 30
Eje medio = (10 + 30) / 2 = 20
El rango y el eje medio pueden ser útiles para tener una idea general del conjunto de datos, pero no proporcionan información detallada sobre la distribución de los valores.
Consejos para interpretar las medidas de tendencia central
Al interpretar las medidas de tendencia central, es importante tener en cuenta que no son una descripción completa del conjunto de datos. Las medidas de tendencia central pueden ocultar información importante sobre la distribución de los valores y la presencia de valores extremos.
Por ejemplo, en el conjunto de datos siguiente:
Datos: 10, 15, 20, 25, 30, 100
La media aritmética es 31.67, lo que sugiere que los datos están en promedio cerca de 30. Sin embargo, el valor extremo de 100 indica que la mayoría de los datos están concentrados en los valores más bajos. En este caso, la mediana sería un valor más representativo.
Es importante considerar el contexto y el propósito del análisis estadístico al interpretar las medidas de tendencia central. En algunos casos, la media aritmética puede ser la medida más adecuada, mientras que en otros casos la mediana o la moda pueden ser más útiles.
Ideas para utilizar las medidas de tendencia central
Las medidas de tendencia central pueden ser útiles en una gran variedad de situaciones. A continuación, se presentan algunas ideas para utilizarlas:
En estadística descriptiva
Las medidas de tendencia central son una herramienta básica en la estadística descriptiva, que se utiliza para resumir, organizar y visualizar conjuntos de datos. Las medidas de tendencia central pueden ser utilizadas para comparar la distribución de valores en dos o más conjuntos de datos, identificar valores atípicos o anomalías y evaluar el grado de simetría o asimetría en la distribución de los valores.
En investigación de mercados
Las medidas de tendencia central son una herramienta valiosa en la investigación de mercados, que se utiliza para analizar datos de encuestas y estudios de opinión. Las medidas de tendencia central pueden ayudar a identificar las preferencias y necesidades de un mercado o población y a comparar la opinión de diferentes grupos o segmentos de la población.
En ciencias naturales
Las medidas de tendencia central son una herramienta esencial en las ciencias naturales, que se utilizan para analizar datos empíricos y experimentales. Las medidas de tendencia central pueden ser utilizadas para identificar patrones en la distribución de los datos, evaluar la significancia estadística de los resultados y comparar la efectividad de diferentes tratamientos o intervenciones.
Cómo calcular las medidas de tendencia central en Excel
Excel es una herramienta útil para calcular y analizar medidas de tendencia central. A continuación, se presentan los pasos para calcular la media, la mediana y la moda en Excel:
Media
- Abre una hoja de cálculo de Excel y coloca los datos en una columna.
- Selecciona la celda donde deseas obtener la media.
- Escribe la fórmula “=PROMEDIO(RANGO)”, donde “RANGO” es el rango de celdas donde se encuentran los datos.
- Pulsa “Enter” para obtener el resultado.
Mediana
- Abre una hoja de cálculo de Excel y coloca los datos en una columna.
- Selecciona la celda donde deseas obtener la mediana.
- Escribe la fórmula “=MEDIANA(RANGO)”, donde “RANGO” es el rango de celdas donde se encuentran los datos.
- Pulsa “Enter” para obtener el resultado.
Moda
- Abre una hoja de cálculo de Excel y coloca los datos en una columna.
- Selecciona una celda donde desees obtener la moda.
- Escribe la fórmula “=MODA(RANGO)”, donde “RANGO” es el rango de celdas donde se encuentran los datos.
- Pulsa “Enter” para obtener el resultado.
En conclusión, las medidas de tendencia central son un conjunto de herramientas estadísticas que permiten resumir, analizar e interpretar datos. La media aritmética, la mediana y la moda son las medidas de tendencia central más comunes, mientras que el rango y el eje medio proporcionan información adicional sobre el conjunto de datos. Es importante utilizar las medidas de tendencia central con cuidado y tener en cuenta el contexto y el propósito del análisis estadístico.
 Moda y Estilo Las mejores ideas de Estilo de moda
Moda y Estilo Las mejores ideas de Estilo de moda


