
¡Hola amigos! Hoy les hablaremos sobre un tema muy interesante, las medidas de tendencia central para datos no agrupados. Si bien a primera vista puede sonar complicado, no lo es tanto. En este post les explicaremos de manera sencilla lo que son y cómo se calculan estas medidas.
Table of Contents
Medidas de tendencia central: ¿qué son?
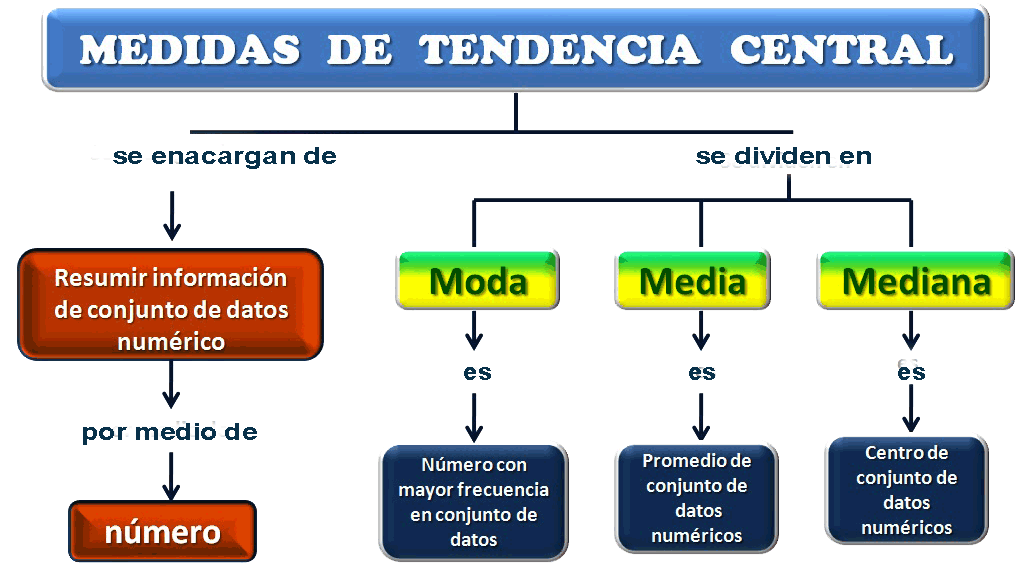
Las medidas de tendencia central son valores que representan en cierto modo la distribución de un conjunto de datos. Se utilizan para describir el centro de los datos, es decir, su valor más típico. Las medidas de tendencia central incluyen la media aritmética, la mediana y la moda.
Media aritmética
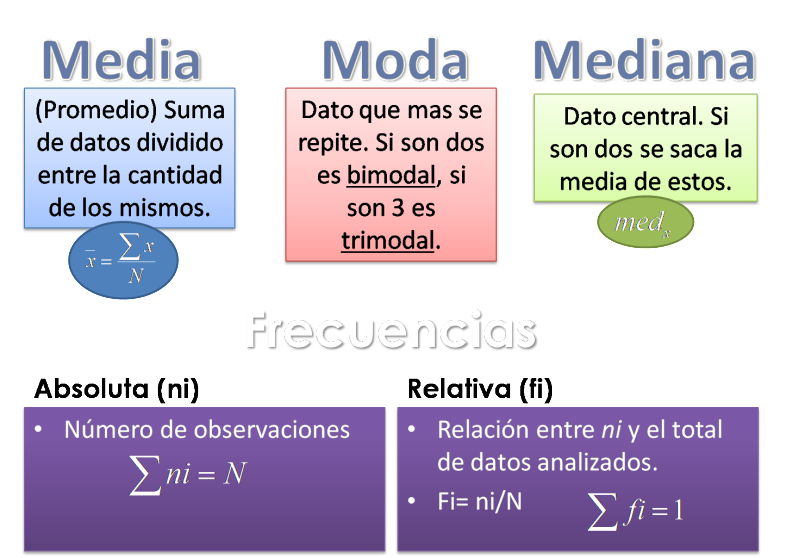
La media aritmética es la medida de tendencia central más comúnmente usada. Se calcula sumando todos los valores de la distribución y dividiendo el resultado entre el número de valores. En otras palabras:
Media aritmética = (valor 1 + valor 2 + valor 3 + … + valor n) / n
Donde n es la cantidad de valores en la distribución.
La media aritmética es muy útil para datos simétricos, es decir, para distribuciones en las que los valores se agrupan alrededor de un punto central. Sin embargo, es sensible a valores extremos o atípicos, lo que puede dar lugar a valores de media que no son representativos de la distribución en su conjunto.
Mediana
La mediana es el valor que se encuentra en el centro de una distribución de datos una vez que estos han sido ordenados. Para calcular la mediana, se debe seguir los siguientes pasos:
- Ordenar los datos de menor a mayor o de mayor a menor.
- Si el conjunto de datos es par, se calcula la media aritmética de los dos valores centrales. Si el conjunto de datos es impar, se toma el valor central.

La mediana es menos sensible a valores extremos que la media aritmética, lo que la hace especialmente útil para conjuntos de datos con valores muy dispersos. Sin embargo, la mediana puede subestimar o sobrestimar la distribución de datos en función de la forma de la distribución.
Moda
La moda es el valor que se presenta con mayor frecuencia en una distribución de datos. En otras palabras, es el valor que más se repite en una serie de datos. Por ejemplo, si tienes los siguientes datos:
[2, 4, 6, 6, 7, 8, 9, 9, 9, 10, 10]La moda sería 9, ya que es el valor que aparece en la serie con mayor frecuencia.

La moda se utiliza sobre todo en distribuciones asimétricas, es decir, en aquellas en las que los valores no se agrupan alrededor de un punto central. Sin embargo, al igual que la media aritmética, la moda puede verse afectada por valores extremos.
Consejos para el cálculo de medidas de tendencia central
Algunos consejos generales para el cálculo de medidas de tendencia central incluyen:
- Es importante conocer la naturaleza de los datos para elegir la medida de tendencia central más adecuada.
- Las medidas de tendencia central se deben usar junto con otras medidas de dispersión para tener una idea completa de la distribución de datos.
- Es recomendable utilizar más de una medida de tendencia central para obtener una imagen más completa de la distribución de datos.
- Si se utilizan medidas de tendencia central para comparar distribuciones de datos, es importante que los datos se midan en las mismas unidades.
Ideas para poner en práctica
Si quieres poner en práctica lo aprendido sobre medidas de tendencia central, puedes intentar lo siguiente:
- Calcular la media aritmética, mediana y moda de un conjunto de datos.
- Comparar las medidas de tendencia central de dos o más conjuntos de datos.
- Investigar diferentes situaciones en las que se utilicen medidas de tendencia central.
¿Cómo interpretar las medidas de tendencia central?
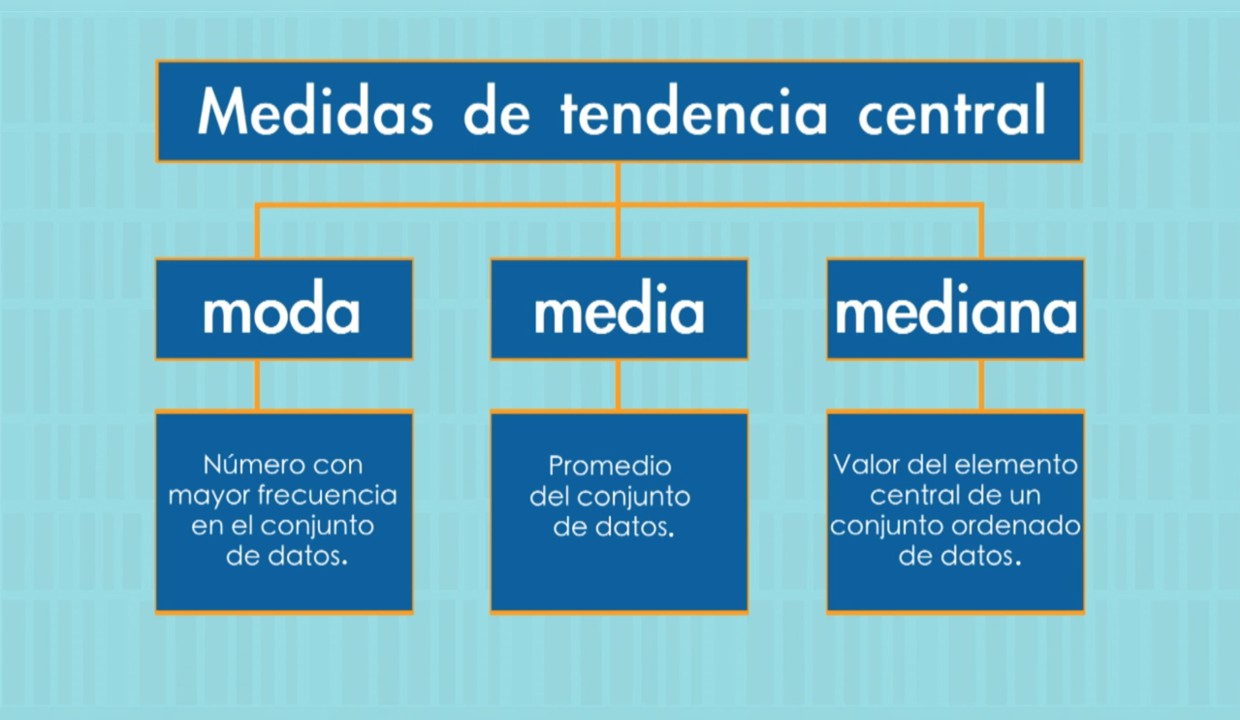
La interpretación de las medidas de tendencia central depende de la naturaleza de los datos. Por lo general, se considera que la media aritmética representa el valor más típico de una distribución de datos, mientras que la mediana representa el valor central y la moda representa el valor más frecuente. Sin embargo, es importante tener en cuenta que cada medida de tendencia central tiene sus limitaciones y no siempre representará la distribución de datos de manera precisa.
En resumen, las medidas de tendencia central son una herramienta útil para describir el centro de una distribución de datos. La media aritmética, la mediana y la moda son las medidas de tendencia central más comunes y se utilizan para diferentes tipos de distribuciones de datos. Al interpretar estas medidas, es importante tener en cuenta la naturaleza de los datos y las limitaciones de cada medida de tendencia central.
Esperamos que este post les haya sido útil para comprender mejor las medidas de tendencia central. Si tienen alguna pregunta o comentario, no duden en escribirnos. ¡Hasta la próxima!

PD: Recuerden que estas medidas también son importantes a la hora de hacer pruebas como el ICFES o en cualquier examen que involucre estadística.
Porqué son importantes Medidas de Tendencia Central
Las medidas de tendencia central son una herramienta fundamental en la estadística descriptiva, ya que con ellas podemos describir en valores exactos, qué tan central es un conjunto de datos; es decir, su promedio o centro, siempre y cuando sean datos no agrupados.
En términos educativos, estas medidas son imprescindibles en la elaboración, calificación y análisis de pruebas de selección múltiple donde se busca obtener un puntaje total que refleje de manera precisa la capacidad de los estudiantes.
En la vida cotidiana, se utilizan sobre todo para describir características comunes de un conjunto de datos, como en el caso de los servicios de salud, que utilizan estas medidas para estimar las necesidades de pacientes y asignar recursos en el sector.
Conclusión
Las medidas de tendencia central son una herramienta fundamental en la estadística descriptiva. A través de ellas podemos obtener información clave sobre el centro de un conjunto de datos, siempre y cuando sean datos no agrupados. La media aritmética, la mediana y la moda son las medidas de tendencia central más comunes, cada una útil para diferente tipo de distribuciones de datos. Es importante tener en cuenta la naturaleza de los datos y las limitaciones de cada medida de tendencia central al interpretarlas. Esperamos que este post les haya sido útil para comprender mejor las medidas de tendencia central. ¡Hasta la próxima!
 Moda y Estilo Las mejores ideas de Estilo de moda
Moda y Estilo Las mejores ideas de Estilo de moda

