Medidas De Tendencia Central Moda Y Mediana

¡Hola a todos! Hoy hablaremos sobre un tema muy interesante, las medidas de tendencia central. Seguramente ya habrás oído hablar de ellas, pero ¿sabes en qué consisten? Pues bien, son herramientas estadísticas que nos permiten conocer la distribución de los datos, es decir, si hay valores que se repiten con mayor frecuencia, si predominan los valores altos o bajos, etc.

Para explicarlas, empezaremos por la media. Ésta es el valor obtenido al sumar todos los datos y dividir el resultado entre el número de datos. Se puede representar mediante la fórmula:

Media = (x1+x2+…+xn)/n

Por ejemplo, si tenemos los siguientes datos: 2, 4, 6, 8 y 10, su media sería:

Media = (2+4+6+8+10)/5 = 6

¡Muy bien! Ahora, pasemos a la mediana. La mediana es el valor que se encuentra en el centro de la distribución de datos, es decir, que separa al conjunto de datos en dos grupos iguales. Para encontrarla, debemos ordenar los datos de menor a mayor y buscar el valor central. En caso de haber un número par de datos, se calcula la media de los dos valores centrales.

Veamos un ejemplo. Supongamos que tenemos los siguientes datos: 2, 4, 6, 8, 10 y 12. En este caso, la mediana sería:

Mediana = 8

Ya que es el valor central de la distribución de datos. Si en cambio tuviésemos un número par de datos, por ejemplo: 2, 4, 6, 8, 10, 12, la mediana sería:

Mediana = (6+8)/2 = 7

Ya que es la media de los dos valores centrales.

Por último, hablaremos sobre la moda. La moda es el valor que se repite con mayor frecuencia en la distribución de datos. Puede haber una moda, varias o ninguna. Es importante destacar que la moda sólo se aplica a datos discretos, es decir, aquellos que toman valores enteros.

Para encontrar la moda, basta con contar cuántas veces se repite cada valor en la distribución de datos y quedarnos con el que se repite con mayor frecuencia. Si hay varios valores que se repiten con la misma frecuencia, decimos que hay varias modas.

Ahora que ya conoces las tres medidas de tendencia central, es importante destacar que no siempre son iguales en una misma distribución de datos. Por ejemplo, una distribución simétrica (en la que los valores se reparten de manera equitativa a ambos lados de la media) tendrá la media, mediana y moda iguales. Pero si la distribución está sesgada hacia un lado, es posible que éstas difieran entre sí.

En resumen, las medidas de tendencia central son herramientas estadísticas que nos permiten conocer en qué punto se concentra la distribución de datos. La media es el valor obtenido al sumar todos los datos y dividir entre el número de datos, la mediana es el valor central de la distribución de datos y la moda es el valor que se repite con mayor frecuencia en la distribución de datos.

Espero que esta explicación haya sido de utilidad para ti. Ahora, te dejamos con unas imágenes y consejos para que puedas practicar y mejorar tus conocimientos sobre las medidas de tendencia central.

Imagen 1

En esta imagen podemos ver un ejemplo de cómo se calculan la media, mediana y moda a partir de una distribución de datos.

Consejos para calcular la media

• Si tienes datos atípicos, considera eliminarlos antes de hacer el cálculo de la media.
• Cuando los datos son pocos, la media puede no ser representativa de la distribución de datos.

Imagen 2

En esta imagen podemos ver un ejemplo de cómo se ordenan los datos para calcular la mediana a partir de una distribución de datos.

Consejos para calcular la mediana

• Si la distribución de datos es simétrica, la mediana coincide con la media.
• Si tienes un número par de datos, asegúrate de calcular la media de los dos valores centrales.

Imagen 3

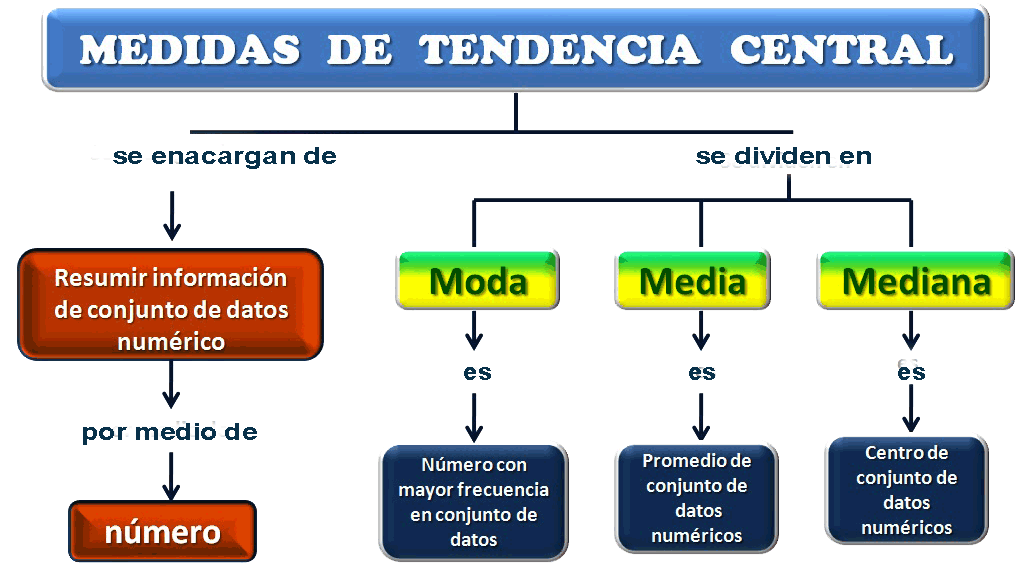
En esta imagen podemos ver un ejemplo de cómo se identifica la moda a partir de una distribución de datos.

Consejos para identificar la moda

• La moda sólo se aplica a datos discretos, es decir, aquellos que toman valores enteros.
• Puede haber una moda, varias o ninguna.

Esperamos que estos consejos y ejemplos te ayuden a mejorar tus conocimientos sobre las medidas de tendencia central. No dudes en practicar y realizar ejercicios para afianzar tus conocimientos. ¡Hasta la próxima!