¡Hola a todos! ¿Alguna vez has tenido que recopilar y analizar datos? Hoy en día, la estadística es una habilidad muy importante, especialmente en el trabajo y en la vida cotidiana. Para poder manejar adecuadamente los datos que se nos presentan, necesitamos comprender las medidas de tendencia central y dispersión. Es por eso que hoy te traemos esta increíble guía sobre las medidas de posición, de tendencia central y de dispersión. ¡Así que, quédate con nosotros y aprendamos juntos!
Table of Contents
Medidas de Posición
Antes de llegar a las medidas de tendencia central y dispersión, es importante comprendender las medidas de posición. Las medidas de posición son simplemente una forma de organizar los datos de un conjunto en orden, para que podamos determinar la posición relativa de un dato. Las dos medidas de posición más comunes son la mediana y el percentil.
Mediana
La mediana es el valor que se encuentra justo en el centro de los datos. Es decir, el punto donde la mitad de los datos son menores y la otra mitad son mayores. Para calcular la mediana, se deben ordenar los datos de menor a mayor y seleccionar el valor del medio.
Consejos:
- La mediana es más útil que la media cuando los datos son asimétricos o si hay valores extremos que pueden distorsionar la media.
Percentil
Un percentil es el valor por debajo del cual cae un porcentaje dado de los datos. Por ejemplo, el percentil 50 es la mediana, el valor debajo del cual el 50% de los datos aparece. La mediana es el percentil 50.

Consejos:
- Los percentiles son muy útiles para comparar datos o para establecer si un punto de datos es “normal” o “anormal”.
Medidas de Tendencia Central
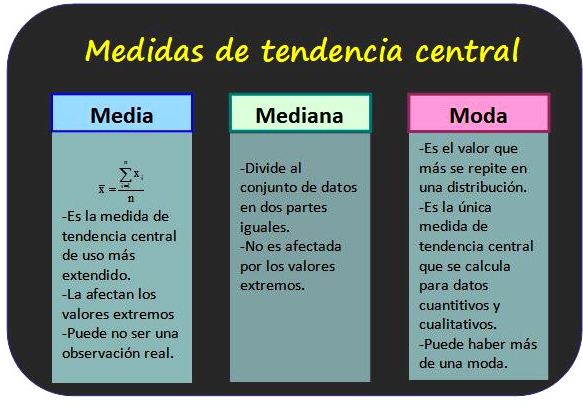
Las medidas de tendencia central indican el valor central alrededor del cual se agrupan los datos. La media, la mediana y la moda son los tres tipos de medidas de tendencia central más utilizados.
Media
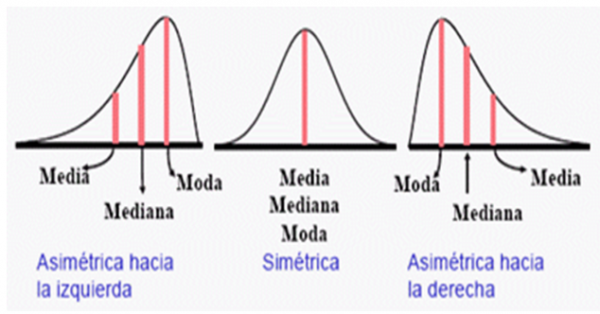
La media es la suma de todos los valores dividido por el número de valores. La media representa el valor central de un conjunto de datos. Si tienes un conjunto de datos simétricos, la media y la mediana serán iguales.
Consejos:
- La media es más útil que la mediana cuando los datos son simétricos.
- La media es sensible a los valores atípicos en los datos.
Mediana
Como mencionamos anteriormente, la mediana es el valor central cuando los datos se organizan de menor a mayor. Se utiliza especialmente cuando hay datos asimétricos o variables atípicas. La mediana no se “ve” influenciada por las variables atípicas.

Consejos:
- La mediana es más útil que la media cuando los datos son asimétricos o si hay valores extremos que pueden distorsionar la media.
Moda
La moda es el valor que se produce con más frecuencia en un conjunto de datos. La moda es útil cuando se quiere calcular el valor más común. Hay varias modas para diferentes distribuciones de datos.
Consejos:
- La moda se utiliza cuando se quiere saber la tendencia de los datos.
- La moda no tiene en cuenta todas las observaciones de los datos.
Medidas de Dispersión
Las medidas de dispersión se utilizan para indicar qué tan dispersos o agrupados están los datos. Las medidas de dispersión incluyen el rango, la varianza y la desviación estándar.
Rango
El rango es la diferencia entre el valor máximo y el valor mínimo de un conjunto de datos.

Consejos:
- El rango es útil para medir la variabilidad en los dato.
- El rango no es muy útil para conjuntos de datos con observaciones atipicas.
Varianza
La varianza es otra medida de dispersión y se utiliza para describir cómo se distribuyen los datos alrededor de la media.

Consejos:
- La varianza es útil cuando queremos obtener una idea de cuánto varían los datos.
- La varianza es sensible a las observaciones atípicas y puede dar lugar a valores muy grandes.
Desviación estándar
La desviación estándar es la raíz cuadrada de la varianza y se utiliza para medir qué tan dispersos están los datos. Es la medida de la propagación de los datos.
Consejos:
- La desviación estándar se utiliza cuando se quiere saber qué tan uniforme es la distribución de los datos.
- La desviación estándar puede ser engañosa si los datos son muy dispersos.
Cómo Usar las Medidas de Tendencia Central y Dispersión
Ahora que ya sabes lo que son las medidas de tendencia central y dispersión, aquí te dejamos algunos consejos para aplicar estas medidas a conjuntos de datos:
Ideas:
- Elige la medida de tendencia central más apropiada según la distribución de los datos.
- Utiliza los percentiles para comparar los datos con otros conjuntos de datos.
- Elige la medida de dispersión más apropiada según la distribución de los datos.
Conclusión
¡Y así es como terminamos! Esperamos que esta guía te haya ayudado a comprender la importancia de las medidas de tendencia central y dispersión. Ahora, debes ser capaz de aplicar estas medidas a conjuntos de datos y sacar conclusiones basadas en esta información. No olvides ser constante y aplicar estas medidas siempre que las necesites. ¡Mucho éxito!
 Moda y Estilo Las mejores ideas de Estilo de moda
Moda y Estilo Las mejores ideas de Estilo de moda

