
¡Hola a todos! Hoy vamos a hablar sobre la estadística y las medidas de tendencia central. Si eres un estudiante que se está preparando para un examen de matemáticas o simplemente tienes curiosidad sobre el tema, ¡este artículo es para ti!
La estadística es una rama de las matemáticas que se usa para recopilar, analizar e interpretar datos. Hay muchas formas de describir los datos, pero una forma común es mediante medidas de tendencia central. Estas medidas resumen los datos y nos dicen qué valores son más comunes o representativos en un conjunto de datos.
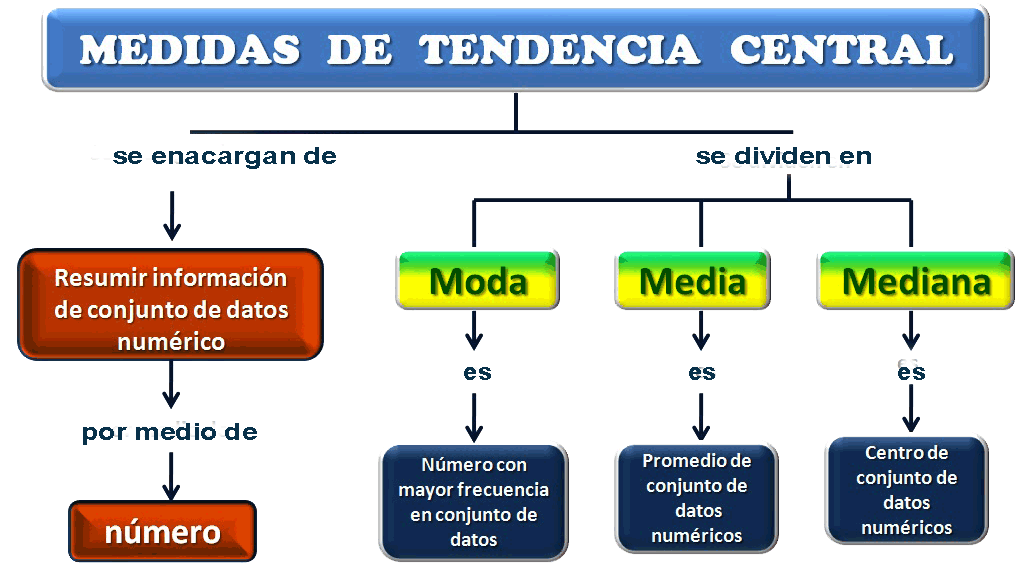
Podemos encontrar tres medidas de tendencia central: la media, la mediana y la moda. ¡Veamos cada una de ellas!
Table of Contents
Media
La media se calcula sumando todos los valores en un conjunto de datos y dividiendo ese número por el total de valores en el conjunto. Entonces, la media es el valor promedio en el conjunto de datos.
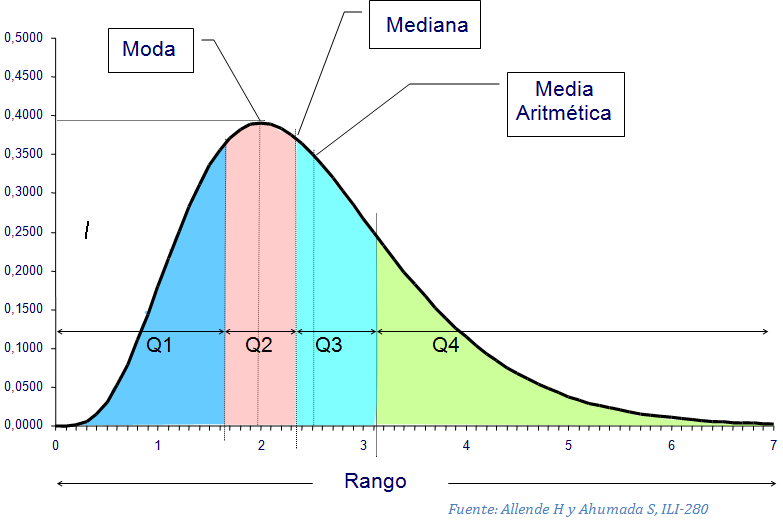
La media es una medida común de tendencia central y es especialmente útil cuando los datos tienen una distribución normal. Una distribución normal es una distribución de datos donde la mayoría de los valores se encuentran cerca de la media.
Como consejo, recuerda que la media puede ser afectada por valores extremos o atípicos en un conjunto de datos. Si hay valores extremos en tu conjunto de datos, considera usar la mediana en su lugar.
Mediana
La mediana es el valor en el medio de un conjunto de datos ordenados de menor a mayor (o viceversa). Es decir, si tienes un conjunto de 7 datos, la mediana sería el cuarto valor en los datos ordenados de menor a mayor.

La mediana es una medida útil cuando los datos tienen valores extremos o cuando los datos no tienen una distribución normal. También es útil cuando el conjunto de datos es pequeño.
Como idea, si quieres calcular la mediana para un conjunto de datos impares, simplemente encuentra el valor en la posición (n+1)/2 en un conjunto de datos ordenados. Para un conjunto de datos par, encuentra los dos valores en las posiciones n/2 y (n/2)+1 y calcula su media.
Moda
La moda es el valor más común en un conjunto de datos. Es decir, la moda es el valor que aparece con más frecuencia en el conjunto de datos.

La moda es una medida útil cuando quieres encontrar el valor más común en un conjunto de datos. Puede haber más de una moda en un conjunto de datos si varios valores tienen la misma frecuencia.
Como consejo, recuerda que la moda no siempre es útil para describir la forma de una distribución de datos. Un conjunto de datos puede tener varias modas y aún no tener una distribución normal.
Ahora que ya sabes qué son las medidas de tendencia central, ¡es hora de aprender cómo calcularlas!
Cómo calcular medidas de tendencia central
Para calcular la media, simplemente suma todos los valores en el conjunto de datos y divídelos por el total de valores en el conjunto. Por ejemplo, si tienes un conjunto de datos con los valores 2, 4, 5, 7 y 8, la media sería:
(2+4+5+7+8)/5 = 26/5 = 5.2
Para calcular la mediana, debes ordenar los valores de menor a mayor (o viceversa) y encontrar el valor medio en el conjunto de datos ordenados. Por ejemplo, si tienes un conjunto de datos con los valores 2, 3, 5, 7 y 8, la mediana sería:
la posición (n+1)/2: (5+1)/2 = 3
El tercer valor en el conjunto ordenado es 5, por lo que la mediana es 5.
Para calcular la moda, debes encontrar el valor que aparece con más frecuencia en el conjunto de datos. Por ejemplo, si tienes un conjunto de datos con los valores 1, 4, 4, 7, 8 y 8, la moda sería:
4 y 8 porque ambos valores son los que más se repiten.
Como consejo final, recuerda que las medidas de tendencia central son solo una forma de describir los datos en un conjunto. A menudo es importante tener en cuenta otras medidas de dispersión o distribución de los datos, como la desviación estándar o el rango intercuartil.
Esperamos que hayas encontrado útil este artículo sobre las medidas de tendencia central. Si tienes más preguntas o necesitas ayuda con problemas específicos en matemáticas, no dudes en consultarnos. ¡Hasta la próxima!




 Moda y Estilo Las mejores ideas de Estilo de moda
Moda y Estilo Las mejores ideas de Estilo de moda


