
¡Hola chicos y chicas! ¿Cómo están? Hoy quiero hablarles sobre un tema que es muy importante en estadística: las medidas de tendencia central. Les voy a mostrar algunos ejercicios resueltos y ejemplos para que puedan entender mejor de qué se trata.
Table of Contents
Ejercicios Medidas De Tendencia Central – Estudiar
En este ejercicio vamos a calcular la media, la mediana y la moda de un conjunto de datos. Los datos son los siguientes: 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70.
Primero vamos a calcular la media. Para hacerlo, sumamos todos los datos y los dividimos por la cantidad de datos. En este caso, la suma es 510, y como hay 13 datos, la media es 39.23.
Luego, calculamos la mediana. Para hacerlo, primero debemos ordenar los datos de menor a mayor. En este caso, el orden sería: 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70. Como hay un número impar de datos, la mediana es el número que está en el medio de la lista, es decir, el número 40.
Finalmente, calculamos la moda. La moda es el número que más se repite en la lista. En este caso, no hay ningún número que se repita más que los demás, por lo que no hay moda.
¡Muy bien! Ya sabemos cómo calcular la media, la mediana y la moda en un conjunto de datos. Ahora vamos a ver algunos ejemplos más.
Medidas De Tendencia Central Ejemplos
En este ejemplo vamos a calcular la media, la mediana y la moda de un conjunto de notas de un grupo de estudiantes. Las notas son las siguientes:
- 8
- 9
- 10
- 9
- 8
- 7
- 8
- 10
- 8
- 10

Para calcular la media, sumamos todas las notas y las dividimos por la cantidad de estudiantes. La suma es 87, y como hay 10 estudiantes, la media es 8.7.
Para calcular la mediana, primero debemos ordenar las notas de menor a mayor. En este caso, el orden sería: 7, 8, 8, 8, 8, 9, 9, 10, 10, 10. Como hay un número par de notas, la mediana es el promedio de los dos números que están en el medio de la lista, es decir, (8+9)/2=8.5.
Para calcular la moda, debemos encontrar la nota que más se repite en la lista. En este caso, la nota que más se repite es 8, por lo que la moda es 8.
¡Muy bien! Ya sabemos cómo calcular la media, la mediana y la moda en un conjunto de notas de un grupo de estudiantes. Ahora vamos a ver cómo se usan estas medidas en la vida real.
TOMi.digital – Medidas de tendencia central
TOMi.digital es una plataforma de aprendizaje en línea que ofrece cursos sobre diversos temas. En uno de sus cursos sobre estadística, se explica cómo se utilizan las medidas de tendencia central en la investigación de mercado.

En la investigación de mercado, se recolectan datos sobre los hábitos, gustos y preferencias de los consumidores. Estos datos se analizan utilizando las medidas de tendencia central para obtener información sobre la opinión de la mayoría de los consumidores.
Por ejemplo, si se quiere determinar cuál es el producto preferido de los consumidores de una determinada marca, se puede calcular la media de las calificaciones que le dieron los consumidores a cada producto. El producto con la calificación más alta será considerado el preferido.
Las medidas de tendencia central también se utilizan para estimar la demanda de un producto o servicio. Si se sabe cuál es el promedio de la cantidad de productos que compran los consumidores en un determinado período de tiempo, se puede estimar cuánto se venderá en el futuro.
¡Interesante, verdad? Ahora vamos a ver un mapa conceptual sobre las medidas de tendencia central.
Mapa Conceptual De Medidas De Tendencia Central Necto Images
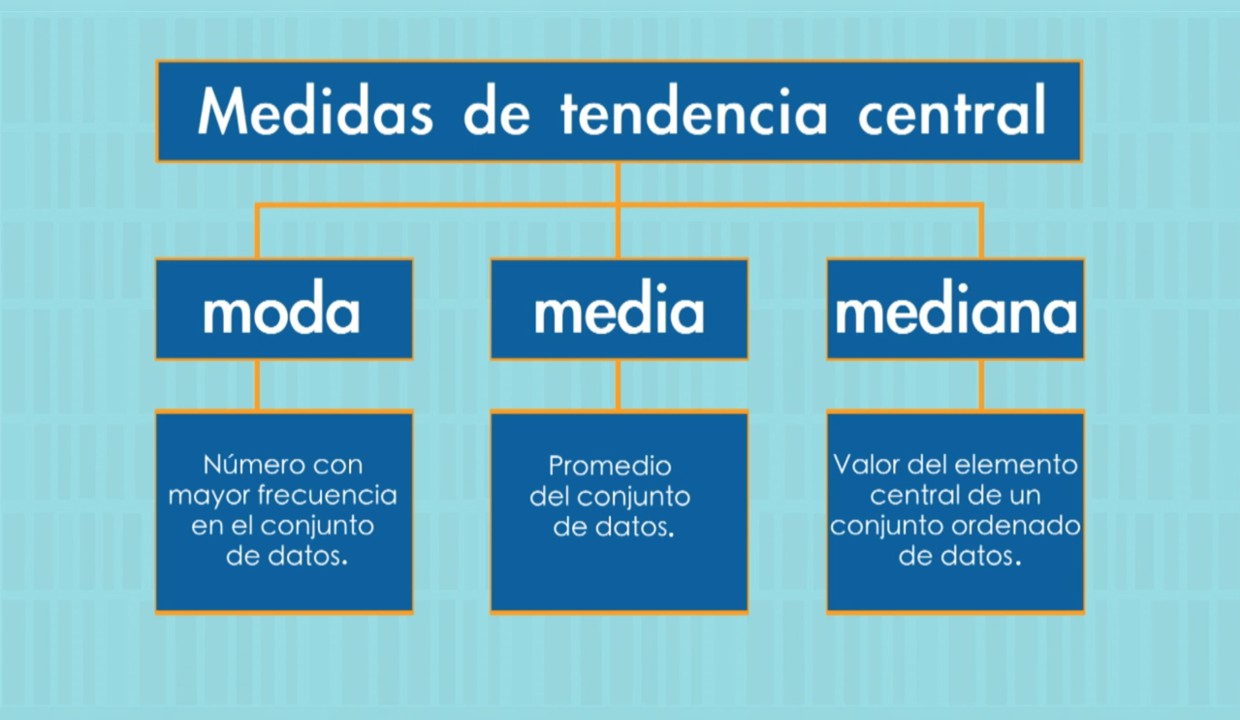
Este mapa conceptual nos muestra de manera clara y sintética qué son las medidas de tendencia central y cómo se calculan.

Como podemos ver en el mapa, la media, la mediana y la moda son las medidas de tendencia central más comunes. También se explica cómo se calculan y en qué casos se usan cada una de ellas.
¡Muy bien! Ya sabemos qué son las medidas de tendencia central y cómo se calculan. Ahora vamos a ver algunos consejos para usarlas correctamente.
MEDIDAS TENDENCIA CENTRAL I ~ HONORIANO MATEMÁTICA
En este video, el profesor Honoriano explica algunos consejos para usar las medidas de tendencia central correctamente.

Uno de los consejos que da el profesor es que siempre se deben tener en cuenta los valores atípicos. Un valor atípico es un dato que se aleja mucho del resto de los datos en la lista. Si hay un valor atípico, puede afectar significativamente el resultado de las medidas de tendencia central.
Otro consejo importante es que se deben usar las medidas de tendencia central apropiadas dependiendo de la distribución de los datos. Si los datos tienen una distribución normal, se puede usar cualquiera de las tres medidas de tendencia central. Si los datos tienen una distribución asimétrica, como una distribución sesgada a la derecha o a la izquierda, se recomienda usar la mediana en lugar de la media.
Finalmente, el profesor recomienda siempre tener en cuenta el contexto en el que se están analizando los datos. Las medidas de tendencia central no son la única forma de analizar los datos, y en algunos casos pueden no ser la mejor opción.
¡Muy buenos consejos! Ahora vamos a ver algunas ideas de ejercicios para practicar el cálculo de las medidas de tendencia central.
Media, mediana y moda – Ficha interactiva
En esta ficha interactiva, puedes practicar el cálculo de la media, la mediana y la moda en un conjunto de datos.

La ficha te presenta un conjunto de datos y te pide que calcules la media, la mediana y la moda. Es una excelente forma de practicar lo que aprendimos en los ejercicios y ejemplos anteriores.
¡Muy bien! Ya sabemos cómo calcular las medidas de tendencia central, cómo se usan en la vida real, algunos consejos para usarlas correctamente y algunas ideas para practicar su cálculo. Ahora vamos a ver un ejemplo más completo que muestra cómo se pueden usar estas medidas para tomar decisiones informadas.
florero Jardines Precaución tendencia central media mediana y moda
En este ejemplo, vamos a ver cómo se pueden usar las medidas de tendencia central para tomar decisiones informadas sobre un negocio de venta de flores.
Supongamos que María tiene un negocio de venta de flores llamado Florero Jardines. Ella ha recopilado datos sobre las ventas de los últimos seis meses, y quiere usar las medidas de tendencia central para tomar decisiones informadas sobre su negocio.
Estos son los datos que ha recopilado:
- Enero: $500
- Febrero: $600
- Marzo: $450
- Abril: $800
- Mayo: $700
- Junio: $550
Primero, María va a calcular la media de las ventas de los últimos seis meses. La media es la siguiente:
Media = (500+600+450+800+700+550)/6 = $616.67
Luego, María va a calcular la mediana de las ventas de los últimos seis meses. Para hacerlo, primero debe ordenar los datos de menor a mayor:
- Marzo: $450
- Junio: $550
- Enero: $500
- Febrero: $600
- Mayo: $700
- Abril: $800
Como hay un número par de datos, la mediana es el promedio de los dos datos que están en el medio de la lista. En este caso, la mediana es:
Mediana = (550+600)/2 = $575
Finalmente, María va a calcular la moda de las ventas de los últimos seis meses. La moda es el valor que se repite más veces en la lista. En este caso, no hay ningún valor que se repita más veces que los demás, por lo que no hay moda.
Ahora que María ha calculado la media y la mediana de las ventas de los últimos seis meses, puede utilizar esta información para tomar decisiones informadas sobre su negocio.
Por ejemplo, si María quisiera establecer un objetivo de ventas mensuales, podría usar la media o la mediana como punto de referencia. Si ella decide establecer el objetivo en $616.67 (la media), sabe que si alcanza ese objetivo, estaría vendiendo tanto como lo hizo en los últimos seis meses. Si decide establecer el objetivo en $575 (la mediana), sabe que estaría vendiendo más que la mitad de los meses, lo cual sería un buen resultado.
¡Muy bien! Ya hemos visto algunos ejercicios y ejemplos de las medidas de tendencia central, cómo se usan en la vida real, algunos consejos para usarlas correctamente y cómo se pueden usar para tomar decisiones informadas. Espero que les haya resultado útil y que sigan aprendiendo mucho más sobre estadística y análisis de datos.
 Moda y Estilo Las mejores ideas de Estilo de moda
Moda y Estilo Las mejores ideas de Estilo de moda


