Tendencia Central Y Dispersión Media Moda Y Mediana

Las medidas de tendencia central son herramientas fundamentales en la estadística para analizar conjuntos de datos y obtener información relevante de ellos. Estas medidas nos permiten conocer el valor central de la distribución de los datos y, por tanto, tener una idea de su posición relativa y de su dispersión.

Medidas de Tendencia Central

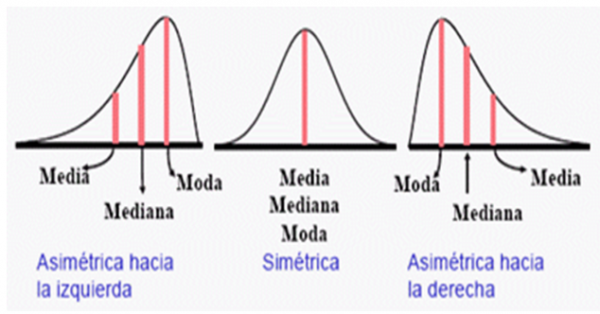
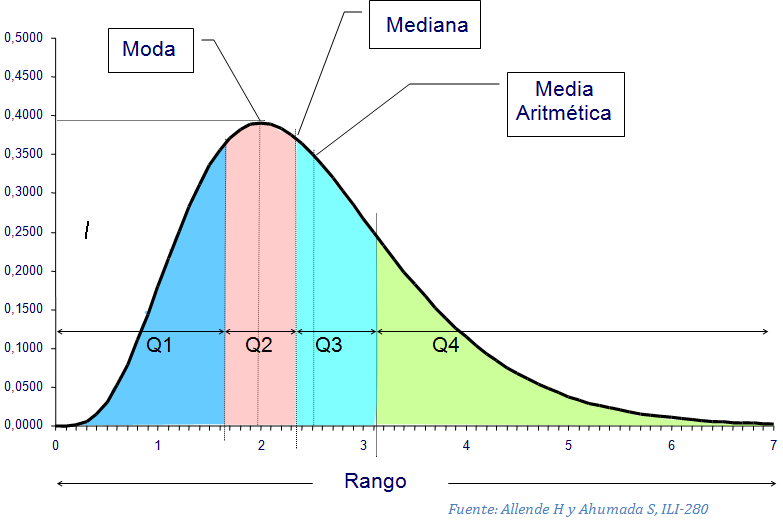
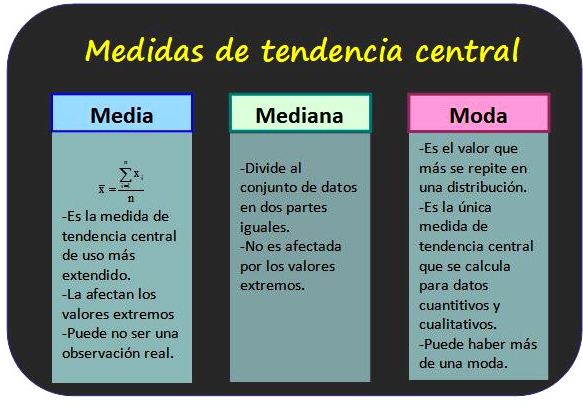
Las medidas de tendencia central más comúnmente utilizadas son la media, la mediana y la moda. La media es la suma de los datos dividida por el número de observaciones. La mediana es el valor central de un conjunto ordenado de datos, es decir, el que divide al conjunto en dos partes iguales. La moda es el valor que más se repite en el conjunto de datos.

Cuál es la medida de tendencia central más adecuada

La elección de la medida de tendencia central más adecuada depende del tipo de distribución de los datos y del objetivo del análisis. Cuando los datos tienen distribución normal, la medida de tendencia central más adecuada es la media, ya que ésta es sensible a todos los valores del conjunto. En cambio, cuando los datos no tienen distribución normal o cuando hay valores atípicos, la mediana puede ser una medida más robusta, ya que es menos sensible a los valores extremos. La moda es adecuada cuando se busca el valor más representativo o cuando se desea identificar patrones en los datos.

Cómo se calculan las medidas de tendencia central

Para calcular la media de un conjunto de datos, se suman todos los valores y se dividen por el número de observaciones:

Media = (x1 + x2 + … + xn) / n

Para calcular la mediana, se ordenan los datos de menor a mayor y se encuentra el valor central. Si el conjunto de datos tiene un número impar de observaciones, el valor central será la mediana; si el conjunto de datos tiene un número par de observaciones, se obtiene la mediana como la media aritmética de los dos valores centrales.

La moda se encuentra identificando el valor que más se repite en el conjunto de datos. Si no hay valores que se repitan, el conjunto se dice que es amodal.

Consejos para el uso adecuado de las medidas de tendencia central

Para obtener resultados precisos y verídicos al utilizar las medidas de tendencia central, es importante seguir ciertos consejos:

• Analiza previamente la distribución de los datos para determinar qué medida de tendencia central es la más adecuada.
• Asegúrate de que los datos sean completos y estén libres de errores o valores atípicos que puedan alterar el resultado.
• Compara las medidas de tendencia central con las medidas de dispersión para tener una mayor comprensión de los datos.
• No te limites a una sola medida de tendencia central, utiliza varias según el propósito del análisis.

Ideas para aplicar las medidas de tendencia central

Las medidas de tendencia central se utilizan en muchos campos, entre ellos:

• En la economía, para estudiar el comportamiento de los mercados y de los precios.
• En la sociología, para analizar las estadísticas vitales, el nivel de vida y otros indicadores sociales.
• En la psicología, para medir variables como la inteligencia, la personalidad y la actitud.
• En la medicina, para estudiar la incidencia de enfermedades y para evaluar tratamientos.

Cómo interpretar las medidas de tendencia central

La interpretación de las medidas de tendencia central depende del contexto del análisis. Por ejemplo, en el análisis de datos económicos, la media de los precios puede ser un indicador del nivel de los precios, mientras que la mediana puede ser un indicador del precio medio de los bienes de consumo. En el análisis sociológico, la media de la edad de los habitantes de una ciudad puede ser un indicador del nivel de envejecimiento de la población, mientras que la mediana puede ser un indicador del nivel de juventud de la población.

Cómo utilizar las medidas de dispersión

Además de las medidas de tendencia central, es importante conocer las medidas de dispersión, que nos permiten conocer la variabilidad de los datos. Las medidas de dispersión más comunes son la desviación estándar, el rango y el coeficiente de variación.

• La desviación estándar es una medida de la variación de los datos respecto a la media. Cuanto mayor sea la desviación estándar, mayor será la variabilidad de los datos.
• El rango es la diferencia entre el valor máximo y el valor mínimo del conjunto de datos. Esta medida de dispersión es sensible a los valores extremos y, por tanto, no es muy robusta.
• El coeficiente de variación es una medida de la variabilidad normalizada por la media. Esta medida es útil para comparar la variabilidad de dos conjuntos de datos que tienen escalas distintas.

Cómo utilizar las medidas de tendencia central y dispersión en conjunto

Para obtener una visión completa de un conjunto de datos, es recomendable utilizar las medidas de tendencia central y las medidas de dispersión en conjunto. Las medidas de tendencia central nos indican el valor central de los datos, mientras que las medidas de dispersión nos indican la variabilidad de los mismos.

Por ejemplo, en el análisis de las notas de un examen, la media nos indica la nota promedio, mientras que la desviación estándar nos indica la variabilidad de las notas en relación a la media. Si la desviación estándar es baja, significa que las notas están muy próximas a la media y que la mayoría de los estudiantes obtuvo una nota similar. Si la desviación estándar es alta, significa que las notas están dispersas y que hubo una gran variabilidad en los resultados.

Conclusiones

Las medidas de tendencia central son herramientas fundamentales para analizar datos y obtener información relevante de los mismos. La elección de la medida de tendencia central adecuada depende del tipo de distribución de los datos y del objetivo del análisis. Es importante conocer también las medidas de dispersión para tener una visión completa de los datos. Para utilizar estas medidas de manera adecuada, es importante seguir ciertos consejos y tener en cuenta el contexto del análisis.

Las medidas de tendencia central se utilizan en muchos campos, desde la economía hasta la medicina, y son indispensables para el análisis de datos en la era de la información. Conociendo cómo utilizar estas medidas, es posible obtener información relevante y tomar decisiones informadas.