¡Hola!, en esta ocasión quiero hablarles sobre un tema importante en estadística, las medidas de tendencia central. En resumen, estas medidas nos permiten encontrar un valor que represente al conjunto de datos y es muy útil en muchos campos como la medicina, la economía, la educación y la investigación en general. A continuación, les mostraré ejemplos de cómo se pueden calcular algunas de estas medidas y por qué son importantes.
Table of Contents
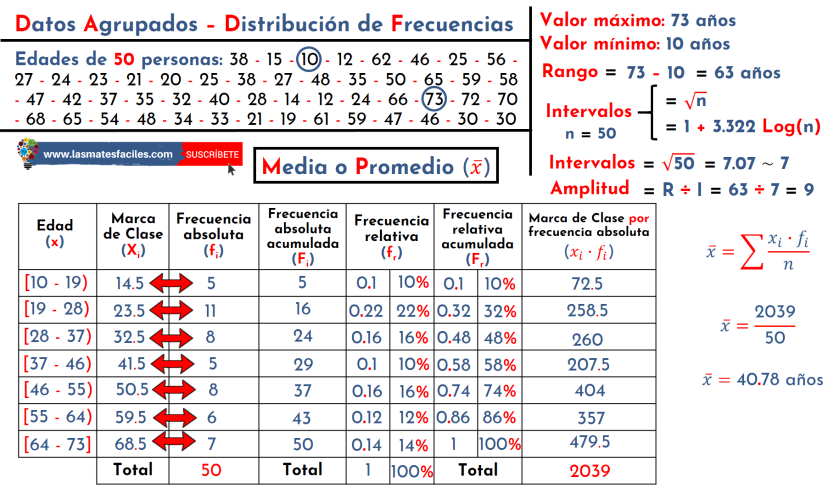
Media aritmética
La media aritmética o promedio, es la suma de todos los datos divididos entre la cantidad de datos. Es una medida muy común y fácil de calcular. Por ejemplo, si tenemos los siguientes datos de notas en un examen:
Podemos calcular la media aritmética como:
(8+6+7+10+9)/5 = 8
Es decir, la media de estas notas es 8. Esta medida es muy útil para analizar el rendimiento en un examen, pero también puede ser utilizada en otros contextos, como el análisis de ingresos, la temperatura, entre otros.
Mediana
La mediana es el valor que divide un conjunto de datos en dos partes iguales. Es decir, si tenemos los mismos datos anteriores:

La mediana sería:
6 7 8 9 10 → Mediana = 8
La mediana es útil cuando tenemos datos atípicos o extremos que afectan la media aritmética. Por ejemplo, si tenemos el siguiente conjunto de datos:
1 2 3 4 400 → Media aritmética = 82, Mediana = 3
Como podemos ver, la media aritmética no es una buena medida en este caso, ya que un solo dato afecta mucho el resultado. En este caso, la mediana es una mejor opción ya que no es afectada por los datos extremos.
Moda
La moda es el valor que se repite con más frecuencia en un conjunto de datos. Por ejemplo, si tenemos los siguientes datos:

Podemos ver que el número 3 se repite dos veces, mientras que los demás números solo aparecen una vez. Entonces, la moda de este conjunto de datos es 3.
La moda es útil en casos donde queremos encontrar el valor más común en un conjunto de datos, por ejemplo, la talla de ropa más vendida en una tienda, el sabor de helado más popular en una heladería, entre otros.
Consejos para el cálculo de medidas de tendencia central
Al calcular las medidas de tendencia central, es importante tener en cuenta algunos consejos que nos ayudarán a obtener resultados precisos:
1. Revisar los datos
Antes de hacer cualquier cálculo, es importante revisar los datos y asegurarnos de que están completos y sin errores. Si encontramos datos faltantes o erróneos, debemos reemplazarlos o eliminarlos, según corresponda.
2. Elegir la medida adecuada
Dependiendo del tipo de datos que tengamos, es importante elegir la medida de tendencia central adecuada. Por ejemplo, la media aritmética es buena para conjuntos de datos equilibrados, mientras que la mediana es mejor para conjuntos con datos extremos.
3. Utilizar fórmulas y herramientas adecuadas
Existen distintas fórmulas y herramientas para calcular las medidas de tendencia central, y es importante elegir la que mejor se adapte a nuestras necesidades y conocimientos. Además, es importante revisar las fórmulas para asegurarnos de que las estamos aplicando correctamente.
Ideas para utilizar medidas de tendencia central
Las medidas de tendencia central son muy útiles en el análisis y toma de decisiones en distintos campos. Algunas ideas para utilizarlas son:
1. Analizar el rendimiento académico
Como vimos anteriormente, podemos utilizar la media aritmética para analizar el rendimiento de los estudiantes en un examen. Además, también podemos utilizar la mediana y la moda para identificar casos de alumnos con notas atípicas o bajos rendimientos.
2. Análisis de datos económicos
Podemos utilizar las medidas de tendencia central para analizar datos económicos como el ingreso promedio de un país, el precio de una mercancía o el costo de una vivienda. Esto nos permitirá identificar tendencias y realizar comparaciones.
3. Análisis de encuestas
Podemos utilizar las medidas de tendencia central para analizar los resultados de una encuesta, identificar las opciones más populares y determinar las preferencias de los encuestados.
Cómo calcular medidas de tendencia central en Excel
Excel es una herramienta muy útil para el cálculo de medidas de tendencia central. A continuación, les mostraré cómo calcular la media, la mediana y la moda en Excel:
Cálculo de la media en Excel
Para calcular la media en Excel, debemos utilizar la fórmula AVERAGE. Si queremos encontrar la media de los datos de la columna B, por ejemplo, debemos seleccionar una celda vacía y escribir la función =AVERAGE(B1:Bn), donde n es el número de la última fila que contiene datos.
Cálculo de la mediana en Excel
Para calcular la mediana en Excel, debemos utilizar la función MEDIAN. Si queremos encontrar la mediana de los datos de la columna B, por ejemplo, debemos seleccionar una celda vacía y escribir la función =MEDIAN(B1:Bn), donde n es el número de la última fila que contiene datos.
Cálculo de la moda en Excel
Para calcular la moda en Excel, debemos utilizar la función MODE. Si queremos encontrar la moda de los datos de la columna B, por ejemplo, debemos seleccionar una celda vacía y escribir la función =MODE(B1:Bn), donde n es el número de la última fila que contiene datos.
En resumen, las medidas de tendencia central son muy útiles para analizar y tomar decisiones a partir de conjuntos de datos. La media, la mediana y la moda son algunas de las medidas más comunes y útiles, pero es importante elegir la medida adecuada según los datos disponibles. Además, Excel es una herramienta muy útil para calcular estas medidas de manera rápida y sencilla. ¡Espero que esta información les sea útil!
 Moda y Estilo Las mejores ideas de Estilo de moda
Moda y Estilo Las mejores ideas de Estilo de moda


