Moda y Estilo Las mejores ideas de Estilo de moda
¡Hola amiguitos! Hoy vamos a hablar de algo de lo que seguro no tienen ni idea: las medidas de tendencia central. ¡Pero no se preocupen! Yo, el genio de la comedia, hice una investigación en internet para explicárselos de la forma más divertida posible. Así que prepárense para aprender y reír a la vez.
Table of Contents
¿Qué son las medidas de tendencia central?
Primero, tenemos que entender qué es eso de la tendencia central. Imaginen que se van de compras con sus amigos y cada uno compra una cantidad diferente de caramelos. La media sería la cantidad que resulta al sumar todos los caramelos y dividirlos entre el número de amigos. Esa cantidad es la tendencia central de los datos, o sea, el valor que representa a todos los demás valores.
¿Ven? No es tan difícil de entender. Ahora, vamos a ver algunas medidas de tendencia central más comunes.
Media aritmética
La media aritmética es lo que acabamos de explicar: la suma de los valores divididos entre su cantidad. Pero, ojo, sólo funciona bien cuando los datos son simétricos y no hay valores extremos. Miren este ejemplo:
Como pueden ver, el valor que representa a los demás es 4, aunque hay valores mucho más altos y mucho más bajos. Si aplicamos la media aritmética, el resultado no es muy útil. ¡Hasta el perro podría saber que algo raro pasa aquí!
Mediana
La mediana es el valor del medio en una lista ordenada. Aunque puede ser un poquito más complicado de aplicar, es una medida más robusta que la media, ya que no se afecta por los datos extremos. Pero, como ven acá, si la cantidad de datos es par, se toma el promedio de los dos valores del medio:
¿Sencillo, no? ¡Si hasta yo lo entendí!
Moda
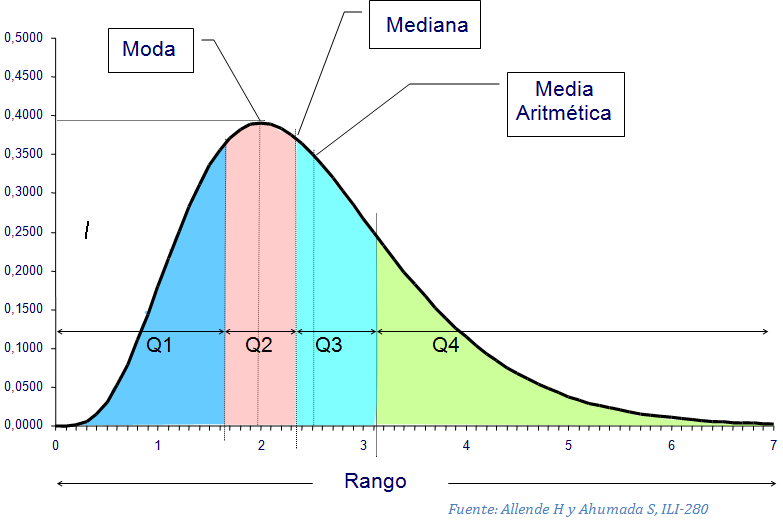
La moda es el valor que más se repite en los datos. Aunque no es muy utilizada por sí sola, puede ayudar a detectar patrones en los datos, como en esta imagen:
No se olviden de que estas medidas no son excluyentes. Se pueden usar juntas para tener una idea más completa de la distribución de los datos.
¿Cómo se calculan?
Como no quiero aburrirlos con la fórmula matemática, aquí les dejo un video de mi amigo Geogebra que les explica cómo aplicar cada medida de tendencia central con la ayuda de la tecnología:
Consejos para entender mejor
Si todavía se sienten un poco perdidos entre tanto número, acá les dejo algunos consejos para que los datos no los asusten:
- Identifiquen qué medida de tendencia central es la más adecuada para sus datos.
- No se confíen sólo de una medida. Usen varias para tener una idea más completa.
- Si tienen que hacer una visualización de sus datos, traten de mostrar las medidas de tendencia central para que sea más fácil de entender.
- ¡Pregunten si no entienden algo! La estadística puede ser complicada, pero nunca es tarde para aprender.
Ideas para practicar
Vamos a hacer un pequeño ejercicio para que vean cómo funciona todo esto. Imaginen que tienen una tienda de juegos donde venden consolas de videojuegos y quieren saber cuánto dinero están ganando en promedio. Estos son los precios que se vendieron ayer:
200, 250, 350, 200, 300, 300, 250, 400, 250, 200
Primero, calculemos la media aritmética:
(200 + 250 + 350 + 200 + 300 + 300 + 250 + 400 + 250 + 200) / 10 = 270
Entonces, el precio promedio fue de 270 pesos. ¿Y la mediana? Primero, ordenamos los precios:
200, 200, 200, 250, 250, 250, 300, 300, 350, 400
Como la cantidad de datos es par, tomamos el promedio de los dos valores de en medio:
(250 + 300) / 2 = 275
Así que la mediana fue de 275 pesos. ¿Y la moda? Pues, acá es fácil de identificar: son los dos precios que más se repitieron, 200 y 250. ¡Listo!
Como siempre, si no les gustó, reclamen acá abajo:
¡Espero que hayan aprendido algo nuevo y se hayan reído un poco conmigo! Para más locuras, sigan mi canal de Youtube, hagan click en el enlace para seguirme en Instagram, o simplemente déjenme un comentario abajo para decirme qué tema les gustaría que trate la próxima vez. ¡Nos vemos en la próxima!
