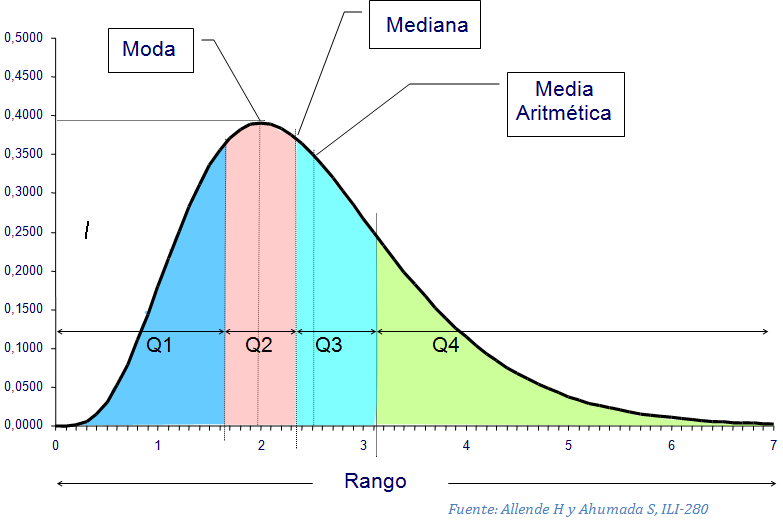
En el mundo de las matemáticas y estadísticas, existen varias medidas que nos ayudan a entender la tendencia central de los datos. La media, mediana y moda son las más comunes y utilizadas en diversos estudios e investigaciones. En este post, exploraremos en detalle cada una de estas medidas y cómo se pueden calcular.
Table of Contents
La media
La media es la medida aritmética de un conjunto de datos y se calcula sumando todos los valores y dividiendo entre la cantidad de datos en esa muestra. Por ejemplo, para el siguiente conjunto de datos: 1, 2, 3, 4, 5, la media sería:
(1 + 2 + 3 + 4 + 5) / 5 = 3
La media es una medida muy útil para entender el promedio del conjunto de datos, aunque es importante considerar que puede ser influenciada por valores extremos.
La mediana
La mediana es el valor que se encuentra en el centro de un conjunto de datos ordenados de menor a mayor o de mayor a menor. Si tenemos un conjunto de datos con un número par de elementos, la mediana se encuentra entre los dos valores centrales y se calcula como la media entre ambos valores. Si el conjunto de datos tiene un número impar de elementos, la mediana es el valor central. Por ejemplo, para el conjunto de datos: 1, 2, 3, 4, 5, la mediana sería 3.
La mediana es útil para entender la distribución central del conjunto de datos, especialmente cuando existen valores extremos o atípicos que podrían afectar la media.
La moda
La moda es el valor o valores que aparecen con mayor frecuencia en un conjunto de datos. Si un conjunto de datos tiene varios valores que aparecen con la misma frecuencia, entonces se dice que el conjunto de datos es bimodal, trimodal, etc. Por ejemplo, para el siguiente conjunto de datos: 1, 2, 2, 3, 3, 3, 4, 5, la moda sería 3.
La moda es útil para entender cuál es el valor más frecuente en un conjunto de datos, lo que puede ser especialmente relevante en estudios de mercado o encuestas de opinión.
Consejos para el cálculo de medidas de tendencia central
Al calcular medidas de tendencia central, es importante considerar los siguientes consejos:
- Asegurarse de que los datos estén organizados correctamente para calcular la mediana o la moda
- Establecer si el conjunto de datos tiene valores extremos o atípicos que podrían afectar la media
- Comprobar que los datos sean representativos de la muestra o población que se está estudiando
- No utilizar una sola medida de tendencia central para entender el conjunto de datos, sino más bien utilizarlas en conjunto para tener una mejor comprensión
Ideas para utilizar medidas de tendencia central
Las medidas de tendencia central son útiles en una variedad de contextos, tales como:
- En investigaciones de mercado para entender la preferencia del consumidor
- En estudios de educación para entender el rendimiento académico de los estudiantes
- En estudios médicos para entender la efectividad de un tratamiento o medicamento
Cómo calcular medidas de tendencia central en Excel
Excel es una herramienta útil para calcular medidas de tendencia central. Para calcular la media, se puede utilizar la función PROMEDIO. Para calcular la mediana, se puede utilizar la función MEDIANA, y para calcular la moda, se puede utilizar la función MODA. Importante tener en cuenta que Excel también tiene funciones para calcular la media, mediana y moda de una distribución normal: MEDIA, MEDIANA y MODO.
En conclusión, las medidas de tendencia central son una herramienta valiosa para entender y analizar conjuntos de datos en una variedad de contextos. Es importante tener en cuenta las diferentes medidas y cómo utilizarlas para tener una comprensión completa y precisa de los datos.
Aprendizaje de la matemática con uso de la TIC: Actividad en geogebra

¿Cuál es la Diferencia entre Moda y Tendencia? Bien Explicado

Ejemplos de cómo calcular la media, mediana y moda, Media, mediana y

Definición de tendencia – Qué es, Significado y Concepto

Medidas De Tendencia Central Ejemplos

Profesor Julio Cesar Sandino: medidas de tendencia central para datos

¿Cuál es la diferencia entre estilo, moda y tendencias? – DM Image

Qué es la unidad estadística ejemplos: Colección de ejemplo images

Medidas De Tendencia Central Mediana Ejemplos Nuevo Ejemplo | Images
 Moda y Estilo Las mejores ideas de Estilo de moda
Moda y Estilo Las mejores ideas de Estilo de moda


