¡Qué onda, gente divertida! ¿Listos para hablar de medidas de tendencia central? ¡Sí, leyeron bien! ¡Hoy vamos a reírnos mientras aprendemos sobre estadística! Así que presta atención, toma un café y disfruta de este viaje por las medidas de posición, tendencia y dispersión.
Table of Contents
Las medidas de tendencia central – Nueva Escuela Mexicana
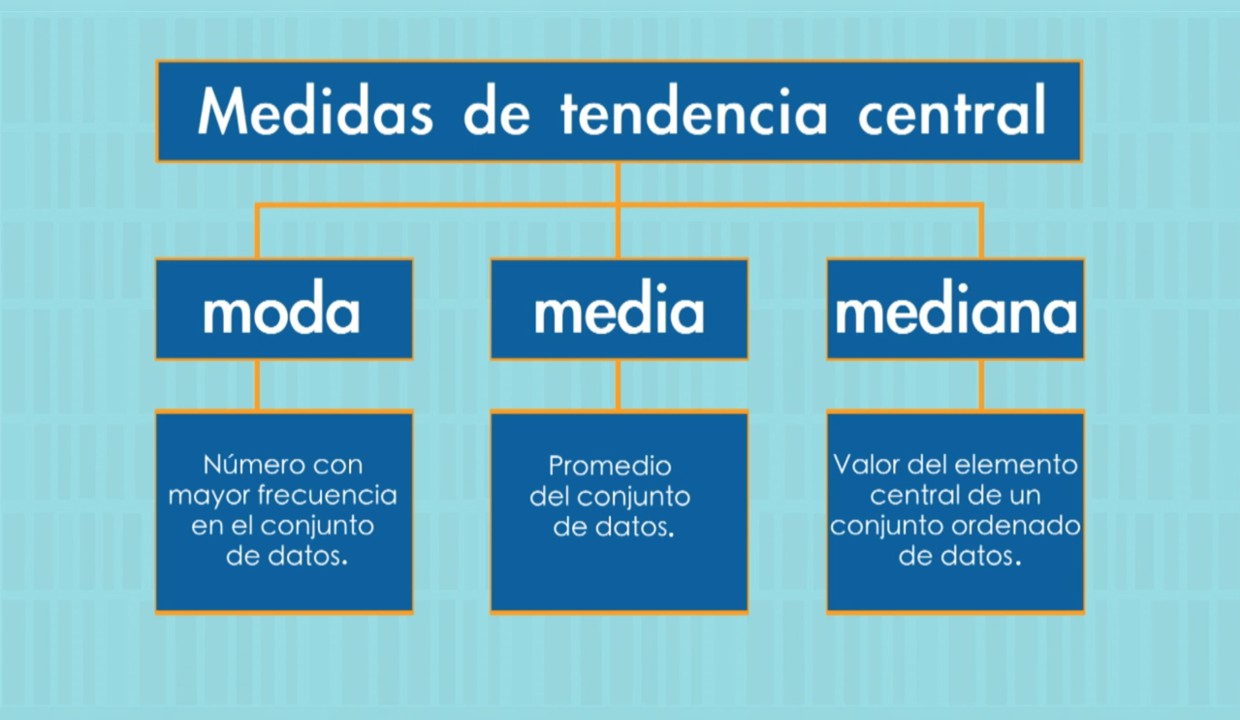
Comencemos con un poco de teoría. En Nueva Escuela Mexicana nos explican que las medidas de tendencia central nos sirven para saber dónde se encuentra el valor medio de un conjunto de datos. Es decir, nos indican si los valores tienden a agruparse alrededor de un número en particular. Hay tres medidas principales: la media, la mediana y la moda.
Media
La media es la suma de todos los valores dividida entre el número de valores. Por ejemplo, si tenemos los siguientes datos: 2, 4, 6, 8, 10, la media sería:
(2 + 4 + 6 + 8 + 10) / 5 = 6
Así que podemos decir que el valor medio de estos datos es 6.
Mediana
La mediana es el valor que ocupa el lugar central en un conjunto de datos ordenados de menor a mayor o de mayor a menor. Si tenemos el siguiente conjunto de datos: 3, 8, 9, 10, 12, la mediana sería 9, ya que es el valor que separa los datos en dos conjuntos de igual tamaño.
Moda
La moda es el valor que aparece con mayor frecuencia en un conjunto de datos. Si tenemos el siguiente conjunto: 8, 5, 2, 5, 9, 5, la moda sería 5, ya que es el valor que se repite con mayor frecuencia.
Interesante, ¿no? ¡Pero esto no es todo! También existen las medidas de posición y dispersión. ¿Quieres saber más? ¡Sigue leyendo!
Medidas de tendencia central ~ Matemáticas y Estadística
Este sitio web nos cuenta que las medidas de tendencia central son muy útiles porque nos permiten representar un conjunto de datos con un solo valor. Además, nos explica que estas medidas no son afectadas por valores extremos en el conjunto de datos. ¡Increíble, ¿verdad?!
Percentiles
Los percentiles son medidas de posición que nos indican qué porcentaje de los datos está por debajo del valor dado. Por ejemplo, el percentil 50 es la mediana, ya que el 50% de los datos está por encima y el 50% por debajo de ese valor.
Varianza
La varianza es una medida de dispersión que nos indica qué tan alejados están los valores del promedio. Si tenemos un conjunto de datos con una gran varianza, significa que los valores están muy alejados del promedio.
Desviación estándar
La desviación estándar es otra medida de dispersión que nos indica qué tan lejos están los valores del promedio. Es la raíz cuadrada de la varianza y se expresa en las mismas unidades que el conjunto de datos.
¡Qué interesante ha sido todo lo que hemos aprendido hasta el momento! Pero todavía nos queda mucho por explorar. ¡Sigue leyendo para descubrir más sobre las medidas de tendencia central y cómo utilizarlas en la vida real!
Medidas de posición, de tendencia central y dispersión
¡Aquí hay más información valiosa sobre estadística! Este sitio web nos explica que las medidas de tendencia central se utilizan para resumir conjuntos de datos. Además, nos dice que estas medidas son muy útiles en la toma de decisiones, ya que nos permiten comparar datos y tomar decisiones informadas.
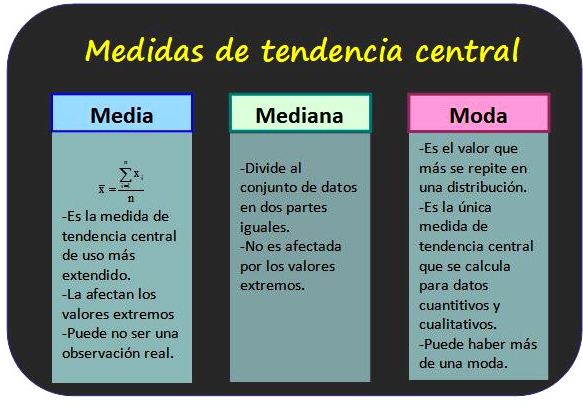
Consejos para interpretar las medidas de tendencia central
1. Si los valores están muy cerca del promedio, la media, la mediana y la moda serán casi iguales.
2. Si los valores están muy alejados del promedio, la media será mayor que la mediana y la moda.
3. Si hay valores extremos en el conjunto de datos, la media se ve afectada más que la mediana y la moda.
Ideas para utilizar las medidas de tendencia central en la vida real
1. En la industria de la moda, se utilizan las medidas de tendencia central para conocer cuáles son los tamaños más populares de ropa.
2. En la industria automotriz, se utilizan las medidas de tendencia central para conocer cuáles son los modelos más populares.
3. En la industria de la música, se utilizan las medidas de tendencia central para conocer cuáles son los géneros más populares.
Cómo calcular las medidas de tendencia central con Excel
Si tienes una hoja de cálculo con los datos que deseas analizar, Excel puede ayudarte a calcular las medidas de tendencia central. Solo necesitas seleccionar los datos, ir a la pestaña “Fórmulas” y luego seleccionar la función correspondiente. Por ejemplo, para calcular la media, debes seleccionar los datos, ir a la pestaña “Fórmulas” y luego seleccionar la función “promedio”.
¡Bien, ya hemos cubierto muchas cosas interesantes! ¿Qué tal si vemos algunos ejemplos de cómo utilizar las medidas de tendencia central en situaciones cotidianas? ¡Vamos allá!
MATEMÁTICA: EJERCICIOS DE MEDIDAS DE TENDENCIA CENTRAL – PROFESORA
En este video de YouTube, una profesora nos explica cómo resolver ejercicios utilizando las medidas de tendencia central. ¡Muy útil para repasar lo que hemos aprendido!

Como resolver problemas de medidas de tendencia central con datos no agrupados
1. Identificar el conjunto de datos.
2. Calcular la media, la mediana y la moda.
3. Interpretar los resultados y sacar conclusiones.
Ejemplo:
Supongamos que tienes el siguiente conjunto de datos: 10, 12, 18, 20, 22, 25. ¿Cuál es la medida de tendencia central que mejor representa los datos?
Primero, debemos calcular la media:
(10 + 12 + 18 + 20 + 22 + 25) / 6 = 16.17
Luego, debemos calcular la mediana:
(18 + 20) / 2 = 19
Finalmente, podemos calcular la moda:
No hay moda en este conjunto de datos, ya que todos los valores son diferentes.
¿Cuál es la medida de tendencia central que mejor representa los datos? En este caso, la mediana sería la mejor opción, ya que es la que divide el conjunto de datos en dos partes iguales.
Medidas de Tendencia Central (Media, Mediana y Moda) – YouTube
En este video de YouTube, podemos ver un ejemplo práctico de cómo utilizar las tres medidas de tendencia central. ¡Muy útil para aquellos a los que les gusta aprender de manera visual!

Como utilizar las medidas de tendencia central en la vida cotidiana
1. Calcular el promedio de los gastos mensuales del hogar para saber cuánto se necesita ahorrar.
2. Calcular la mediana del precio de las casas en una área para tener una idea de cuánto es el precio promedio.
3. Utilizar la moda para tomar decisiones de moda, ya que indica cuáles son las prendas o estilos más populares en la actualidad.
10° PRUEBA TIPO ICFES. MEDIDAS DE TENDENCIA CENTRAL PARA DATOS NO AGRUPADOS
¿Recuerdas cuando hacías pruebas tipo ICFES en la escuela? ¡Bueno, aquí hay otra prueba! Pero no te preocupes, ¡ya tienes todo lo que necesitas para resolverla como un jefe en estadística!

Ejemplo de prueba
Los siguientes son los resultados de un examen de matemáticas:
5, 6, 7, 8, 9
¿Cuál es la mediana?
Primero, debemos ordenar los datos:
5, 6, 7, 8, 9
Luego, podemos calcular la mediana:
(7 + 8) / 2 = 7.5
Por lo tanto, la mediana de este conjunto de datos es 7.5.
¡Genial! Ya hemos aprendido mucho sobre las medidas de tendencia central, su aplicación en la vida real y cómo utilizarlas en situaciones prácticas. ¡No olvides practicar y divertirte mientras aprendes! ¡Hasta la próxima!
 Moda y Estilo Las mejores ideas de Estilo de moda
Moda y Estilo Las mejores ideas de Estilo de moda


