
En el ámbito de la estadística, existen varias medidas de tendencia central que son utilizadas para representar la distribución de un conjunto de datos. Entre estas medidas se encuentran la media, la mediana y la moda. A continuación, vamos a explicar cada una de ellas y cómo se pueden utilizar en diferentes situaciones.
Table of Contents
Media
La media o promedio aritmético es la medida de tendencia central más comúnmente utilizada. Se calcula sumando todos los valores de un conjunto de datos y dividiendo el resultado entre el número total de datos. La media es sensible a los valores atípicos, es decir, aquellos valores que son significativamente diferentes del resto de los valores en el conjunto de datos. Si un conjunto de datos tiene valores atípicos, la media puede no ser una buena representación de la distribución de los datos. En estos casos, es mejor utilizar otras medidas de tendencia central como la mediana o la moda.
Mediana
La mediana es el valor central en un conjunto ordenado de datos. Es decir, es el valor que separa la mitad inferior de la mitad superior de los datos. Si el conjunto de datos tiene un número impar de valores, la mediana será el valor central. Si el conjunto de datos tiene un número par de valores, se calcula promediando los dos valores centrales. La mediana es menos sensible a los valores atípicos que la media, por lo que es una buena medida de tendencia central para conjuntos de datos con valores atípicos.
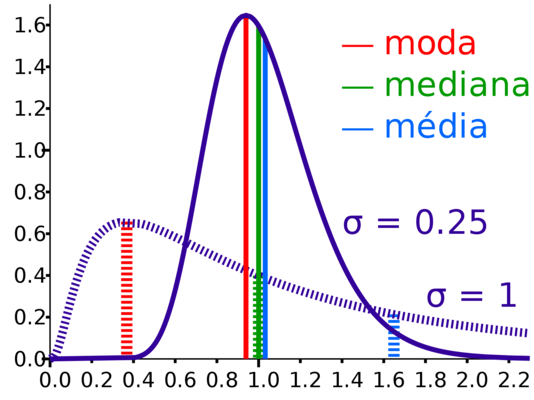
Moda
La moda es el valor que aparece con más frecuencia en un conjunto de datos. Si un conjunto de datos no tiene valores repetidos, no tiene moda. Un conjunto de datos puede tener una moda o varias modas. La moda es adecuada para conjuntos de datos que tienen valores repetidos o datos categorizados.

Las medidas de tendencia central, ya sea la media, la mediana o la moda, son importantes para tener una idea general de qué tan dispersos están los datos para un conjunto de datos particular. Sin embargo, también es importante considerar otras medidas para tener una idea completa de la distribución de datos.
Consejos para el uso adecuado de las medidas de tendencia central
A continuación, se presentan algunos consejos clave para el uso adecuado de las medidas de tendencia central en diferentes situaciones:
1. Identificar los valores atípicos
Es importante identificar los valores atípicos en un conjunto de datos antes de seleccionar la medida de tendencia central adecuada. Si el conjunto de datos tiene valores atípicos significativos, la media podría no representar la distribución de datos de manera adecuada. En estos casos, es mejor utilizar otras medidas de tendencia central, como la mediana o la moda.
2. Considerar el tipo de datos
Es importante considerar el tipo de datos y su naturaleza antes de seleccionar la medida de tendencia central adecuada. Por ejemplo, si los datos son categóricos, la moda podría ser la medida de tendencia central adecuada. Si los datos son continuos, la media o la mediana podrían ser más adecuadas.
3. Combinar diferentes medidas de tendencia central
A menudo, se utilizan diferentes medidas de tendencia central para tener una idea completa de la distribución de datos. Por ejemplo, se puede utilizar la media para identificar la ubicación central de los datos y la mediana para tener una idea de qué tan dispersos están los datos.
Ideas para aplicar las medidas de tendencia central en la práctica
Las medidas de tendencia central tienen numerosas aplicaciones en diferentes campos, como la medicina, la economía, la ingeniería y la psicología. A continuación, se presentan algunas ideas para aplicar las medidas de tendencia central en la práctica:
1. Identificar la edad promedio de los pacientes de un hospital
La media se puede utilizar para calcular la edad promedio de los pacientes de un hospital. Esto puede ser útil para entender la edad de la población del hospital y para planificar los servicios de atención médica adecuados.
2. Determinar la moda de los colores de un producto
La moda se puede utilizar para determinar los colores más populares de un producto. Esto puede ser útil para planificar la producción y el marketing del producto para la próxima temporada.
3. Calcular la mediana de los ingresos anuales de una empresa
La mediana se puede utilizar para calcular los ingresos anuales del personal de una empresa. Esto puede ser útil para identificar a los empleados que se encuentran en diferentes intervalos de ingresos y para planificar políticas salariales adecuadas.
Cómo utilizar las medidas de tendencia central en la práctica
Para utilizar correctamente las medidas de tendencia central en la práctica, se recomienda seguir los siguientes pasos:
1. Identificar el tipo de datos
Antes de seleccionar la medida de tendencia central adecuada, es importante identificar el tipo de datos y su naturaleza. Para datos categóricos, la moda podría ser la medida de tendencia central adecuada. Para datos continuos, la media o la mediana podrían ser más adecuadas.
2. Calcular la medida de tendencia central
Una vez que se ha identificado la medida de tendencia central adecuada, se debe calcular. Para la media, se suman todos los valores y se dividen por el número de datos. Para la mediana, se ordenan los datos y se encuentra el valor que está en el centro. Para la moda, se identifica el valor o valores más frecuentes.
3. Interpretar los resultados
Finalmente, es importante interpretar los resultados de las medidas de tendencia central. Se debe analizar si los datos son representativos de la distribución completa y si las medidas de tendencia central elegidas son adecuadas para el conjunto de datos.
En conclusión, las medidas de tendencia central son herramientas importantes para entender la distribución de los datos y hacer inferencias sobre una población completa. Es importante seleccionar la medida de tendencia central adecuada según la naturaleza de los datos y tener en cuenta otras medidas para tener una idea completa de la distribución de los datos.
 Moda y Estilo Las mejores ideas de Estilo de moda
Moda y Estilo Las mejores ideas de Estilo de moda


