Medidas De Tendencia Central Ejemplos De Moda

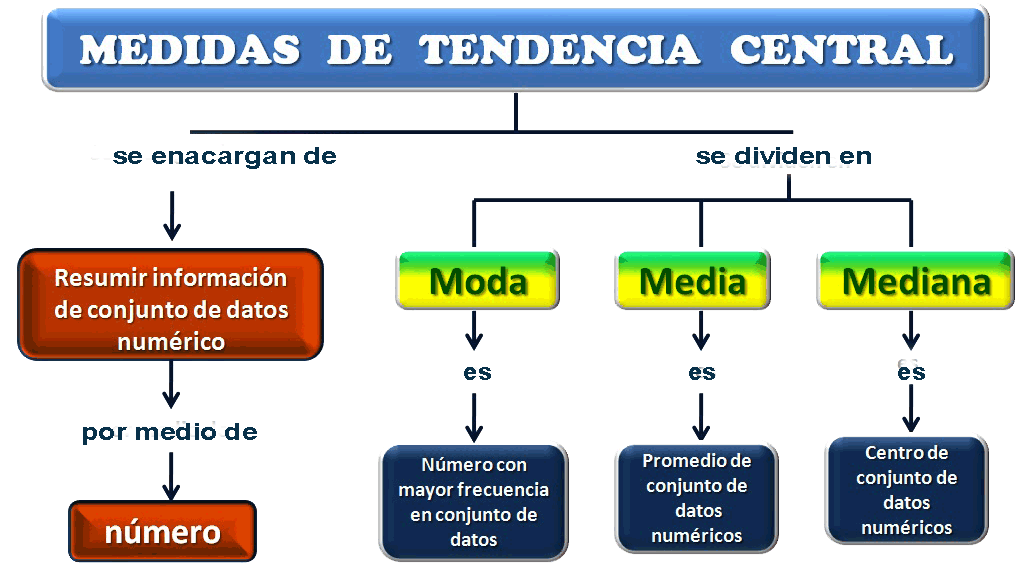
Cuando se habla de medidas de tendencia central, se hace referencia a aquellos valores que representan el centro de una serie de datos. Estas medidas son importantes para el análisis de datos y su interpretación, y es por eso que es necesario conocerlas bien.

Medidas de tendencia central

En estadística existen tres medidas de tendencia central: la media, la mediana y la moda. Cada una de ellas tiene un uso específico dependiendo del tipo de datos que se estén analizando.

Media

La media es la medida de tendencia central más conocida y utilizada. Se calcula sumando todos los valores de la serie de datos y dividiéndolos entre el número total de elementos. La media se representa con la letra griega μ (mu).

La media es una medida sensible a los valores extremos, es decir, aquellos valores que son muy diferentes al resto. Si existen valores extremos en la serie de datos, estos pueden influir en la media y hacer que esta no sea representativa del conjunto de los datos.

Mediana

La mediana es el valor que ocupa la posición central de la serie de datos cuando estos están ordenados de menor a mayor. Si la serie de datos tiene un número par de elementos, la mediana se calcula como la media de los dos valores centrales. La mediana se representa con la letra griega η (eta).

La mediana es una medida menos sensible a los valores extremos que la media, por lo que se utiliza a menudo cuando se tienen datos que se sospecha pueden contener outliers.

Moda

La moda es el valor que se repite con mayor frecuencia en una serie de datos. Puede haber más de una moda, o ninguna si no hay valores que se repitan. La moda se representa con la letra griega ν (nu).

La moda es una medida útil para datos categóricos, es decir, aquellos que no tienen una escala numérica continuada.

Consejos para utilizar las medidas de tendencia central

Es importante ser consciente de las limitaciones de cada una de las medidas de tendencia central y utilizarlas con cautela. Algunas recomendaciones son:

1. Antes de utilizar una medida de tendencia central, asegúrate de que los datos se ajustan a la distribución adecuada.
2. En el caso de la media, comprueba si hay valores extremos que puedan afectar su validez como medida representativa de los datos.
3. Si tienes una serie de datos con valores discretos, como números enteros, utiliza la mediana en lugar de la media.

Ideas para practicar el cálculo de medidas de tendencia central

Para mejorar en el cálculo de medidas de tendencia central, te proponemos algunas ideas:

1. Busca ejercicios y problemas que te permitan practicar el cálculo de la media, la mediana y la moda.
2. Utiliza herramientas estadísticas como Excel o R para calcular estas medidas de forma automatizada.
3. Busca ejemplos reales de la utilización de estas medidas en distintos ámbitos, como pueden ser la economía, la medicina o la psicología.

Cómo utilizar las medidas de tendencia central en la toma de decisiones

Las medidas de tendencia central son útiles para la toma de decisiones en multitud de ámbitos. Algunos ejemplos son:

1. En la empresa, para analizar los resultados de ventas y establecer objetivos.
2. En la industria, para supervisar la calidad de los productos y detectar posibles fallos.
3. En el sector sanitario, para establecer protocolos de tratamiento y detectar patologías.

En definitiva, las medidas de tendencia central son herramientas útiles para el análisis de datos y la toma de decisiones. Es importante conocerlas bien y ser conscientes de sus limitaciones y posibles usos.