Medidas De Tendencia Central Ejemplos Moda Mei

¡Hola chicos y chicas! Hoy vamos a hablar de algo muy divertido (al menos para mí), la estadística. Si, si, lo sé, puede sonar súper aburrido, pero os prometo que vamos a ponernos las gafas de científicos locos y nos lo vamos a pasar genial.

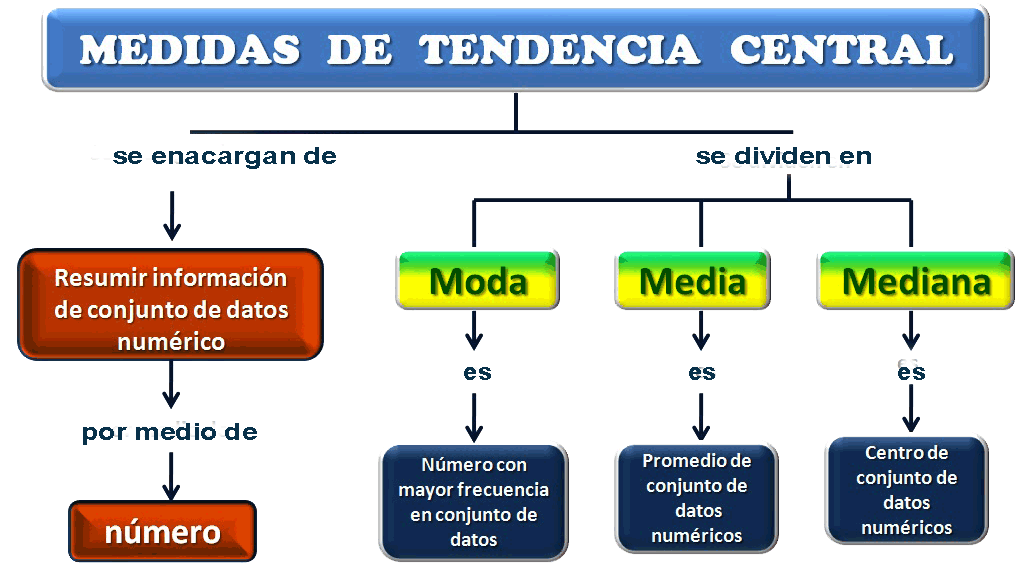
En esta ocasión, vamos a hablar de las medidas de tendencia central. ¿Qué son? Pues son unos trucos que usamos los matemáticos para resumir una colección de datos en un valor que represente el centro o la tendencia de esos datos. Es decir, es una forma de encontrar el valor medio de una serie de números.

Pero no os preocupéis, no necesitamos ser unos Einstein para entenderlo. De hecho, os invito a que os pongáis cómodos, cojáis un lápiz, un papel y nos acompañéis a descubrir todo lo que se esconde detrás de estas medidas.

¡Empecemos ya con los consejos!

Consejos para entender las medidas de tendencia central

Lo primero que necesitamos es una colleción de datos. Puede ser cualquier cosa, desde el número de golpes que se dan en una pelota hasta el número de patitos en un estanque. A partir de ahí, podemos empezar a calcular algunas medidas que nos ayudarán a entender mejor ese conjunto de datos.

Media aritmética

La media aritmética es el valor que resulta de sumar todos los datos y dividirlos entre el número total de datos. Es decir,

Media aritmética = (suma de los datos) / (número total de datos)

Por ejemplo, si tenemos los datos 1, 3, 5, 7 y 9, la media aritmética sería:

Media aritmética = (1 + 3 + 5 + 7 + 9) / 5 = 5

Es importante recordar que para calcular la media aritmética necesitamos que los datos sean numéricos. No podemos calcularla si tenemos, por ejemplo, un conjunto de palabras o nombres.

Mediana

La mediana es el valor que se encuentra en el centro de los datos ordenados de menor a mayor. Es decir, si tenemos los datos 1, 3, 5, 7 y 9, la mediana sería el valor 5.

Si tenemos un número par de datos, la mediana será la media de los dos valores centrales. Por ejemplo, si tenemos los datos 2, 4, 6 y 8, la mediana sería:

Mediana = (4 + 6) / 2 = 5

Moda

La moda es el valor que más se repite en un conjunto de datos. En otras palabras, es el valor que tiene una mayor frecuencia dentro de ese conjunto de datos.

Por ejemplo, si tenemos los datos 1, 1, 3, 3, 3, 5 y 7, la moda sería el número 3, ya que es el que más se repite (tres veces).

Ideas para entender las medidas de tendencia central

Para que sea más fácil entender estas medidas, siempre es bueno poner algunos ejemplos prácticos. Por eso, os propongo algunos ejercicios para que practiquéis vuestras habilidades estadísticas y os divirtáis un rato.

1. Tenemos los siguientes datos: 10, 12, 15, 18, 21 y 25. Calcula la media aritmética y la mediana.

2. Tenemos los siguientes datos: 5, 7, 10, 10, 12, 15, 15, 15, 18, 23. Calcula la moda.

3. En una clase de 25 alumnos, la nota media de un examen es de 7,5. Si se elimina la nota más alta y la nota más baja, la nota media de los restantes es 7,3. ¿Cuál es la nota más alta y la nota más baja?

4. Tenemos los siguientes datos: 3, 3, 3, 3, 3, 3, 3, 3, 8. ¿Cuál es la media aritmética, la mediana y la moda?

5. En una carrera de 10KM, los tiempos de los corredores han sido los siguientes:

45 min, 45 min, 50 min, 55 min, 55 min, 60 min, 60 min, 65 min, 70 min, 70 min.

Calcula la media aritmética, la mediana y la moda.

Como aplicar las medidas de tendencia central

Bueno, ahora que ya sabemos calcular las medidas de tendencia central y tenemos algunos ejemplos a mano, ¿cómo podemos aplicar esto en nuestro día a día? Pues la verdad es que hay muchas situaciones en las que podemos hacer uso de estas herramientas. Algunas de ellas son:

• En estudios de mercado, se puede calcular la media de los precios de un producto para saber cuál es el precio medio que los consumidores estarían dispuestos a pagar.
• En el ámbito de la salud, se pueden calcular las medidas de tendencia central de los niveles de colesterol en una población para saber si es un factor de riesgo importante para enfermedades cardiovasculares.
• En la industria, se pueden calcular las medidas de tendencia central de los tiempos de producción para mejorar la eficiencia y reducir costos de producción.

Como veis, las medidas de tendencia central son muy útiles en muchos ámbitos. Así que, si os gustan las matemáticas y queréis impresionar a vuestros amigos con vuestras habilidades estadísticas, ya sabéis por dónde empezar.

Espero que os hayáis divertido tanto como yo y que hayáis aprendido algo nuevo. Hasta la próxima!