Medidas De Tendencia Central Media Mediana Moda Cuartiles Deciles Percentiles

La estadística es una herramienta muy útil en cualquier ámbito de la vida, desde el trabajo hasta la vida cotidiana. Las medidas de tendencia central son un conjunto de herramientas que se utilizan para obtener una idea general de un conjunto de datos. En este artículo, hablaremos sobre la media, la mediana y la moda para datos agrupados puntualmente.

La media

La media es la suma de todos los valores de un conjunto de datos, dividido por el número de valores en el conjunto. Se denota por la letra griega “μ”. La fórmula para calcular la media es:

Donde:

• x_i son los valores en el conjunto de datos
• n es el número total de valores en el conjunto de datos

Para entender una media para datos agrupados puntualmente, es necesario conocer los conceptos de frecuencia y marca de clase. La frecuencia es el número de veces que se repite cada valor en el conjunto de datos. La marca de clase es el valor central de cada intervalo de clase.

Por ejemplo, supongamos que tenemos los siguientes datos:

Intervalo de clase	Marca de clase	Frecuencia
10 – 19	15	4
20 – 29	25	6
30 – 39	35	5
40 – 49	45	3
50 – 59	55	2
60 – 69	65	1

Para calcular la media de este conjunto de datos, primero tenemos que calcular la marca de clase promedio:

Donde:

• N es el número de intervalos de clase
• x₁ es el límite inferior del primer intervalo de clase
• x_N+1 es el límite superior del último intervalo de clase
• f_i es la frecuencia de la clase

En nuestro ejemplo, el cálculo sería:

Por lo tanto, la marca de clase promedio es 37.5. Ahora podemos calcular la media utilizando la fórmula anterior:

Entonces, la media de este conjunto de datos es 34.5.

La mediana

La mediana es el valor central de un conjunto de datos ordenados. Si hay un número impar de datos, la mediana es el valor del medio. Si hay un número par de datos, la mediana es el promedio de los dos valores centrales.

Para calcular la mediana para datos agrupados puntualmente, necesitamos conocer el número total de datos (n) y la frecuencia acumulada (F_i) de cada intervalo de clase. La frecuencia acumulada es la suma de todas las frecuencias anteriores.

Continuando con nuestro ejemplo, supongamos que tenemos los siguientes datos:

Intervalo de clase	Marca de clase	Frecuencia	Frecuencia acumulada
10 – 19	15	4	4
20 – 29	25	6	10
30 – 39	35	5	15
40 – 49	45	3	18
50 – 59	55	2	20
60 – 69	65	1	21

El número total de datos es 21. La mediana será el valor central de este conjunto de datos, que corresponde al décimo valor (el valor central entre 21 datos). El décimo valor está dentro del intervalo de clase 30-39. Por lo tanto, necesitamos calcular la mediana dentro de este intervalo de clase.

Primero, calculamos el límite inferior del intervalo de clase, que es 30. Luego, calculamos la frecuencia acumulada anterior y la frecuencia del intervalo de clase actual:

• n = 21
• F_i-1 = 10
• f_i = 5
• w = 10
• L = 30

Utilizando la siguiente fórmula, calculamos la mediana:

Por lo tanto, la mediana del conjunto de datos es 33.

La moda

La moda es el valor que ocurre con más frecuencia en un conjunto de datos. Si no hay ningún valor que ocurra con más frecuencia, no hay moda en el conjunto de datos. Un conjunto de datos puede tener una o varias modas.

Para calcular la moda para datos agrupados puntualmente, necesitamos conocer la frecuencia (f_i) y la marca de clase (x_i) de cada intervalo de clase.

Continuando con nuestro ejemplo:

Intervalo de clase	Marca de clase	Frecuencia
10 – 19	15	4
20 – 29	25	6
30 – 39	35	5
40 – 49	45	3
50 – 59	55	2
60 – 69	65	1

El valor de la marca de clase que tiene la frecuencia más alta es 25. Por lo tanto, la moda de este conjunto de datos es 25.

Consejos y trucos

Las medidas de tendencia central son herramientas muy útiles para resumir grandes conjuntos de datos. Sin embargo, no son suficientes para obtener una imagen completa de los datos. Es importante considerar también la varianza, la desviación estándar y otros aspectos de la distribución de datos.

Cuando se utilizan medidas de tendencia central para comparar dos o más conjuntos de datos, es importante considerar también la forma de la distribución (simétrica, sesgada a la izquierda o a la derecha, bimodal, etc.) y otros aspectos de la distribución de datos.

Ideas de aplicación

• Las medidas de tendencia central son muy útiles para resumir grandes conjuntos de datos en una sola cifra. Utilízalas en tu trabajo o en tus investigaciones para obtener una idea general de tus datos.
• Las medidas de tendencia central también son útiles para comparar dos o más conjuntos de datos. Utilízalas para comparar el rendimiento de diferentes productos o servicios, o para comparar los puntajes de diferentes grupos de estudiantes.
• Las medidas de tendencia central también son útiles en la vida cotidiana. Por ejemplo, utilízalas para calcular la edad promedio de tus amigos en una fiesta de cumpleaños, o para obtener una idea del tiempo promedio que tardas en llegar al trabajo.

¿Cómo elegir la medida adecuada?

La elección de la medida de tendencia central adecuada depende del conjunto de datos y del contexto en el que se utilizan. En general, la media es la medida más comúnmente utilizada y es adecuada para conjuntos de datos con una distribución simétrica y sin valores extremos. La mediana es una buena opción cuando el conjunto de datos tiene valores extremos o una distribución sesgada. La moda es adecuada para conjuntos de datos con una distribución “abultada” y con varios valores que tienen la misma frecuencia.

En resumen, las medidas de tendencia central son una herramienta muy útil en la estadística. La media, la mediana y la moda son herramientas importantes para obtener una idea general de un conjunto de datos. Utiliza estas herramientas en tu trabajo, en tus investigaciones y en la vida cotidiana para obtener una idea general de los datos y tomar decisiones informadas.

Imágenes

A continuación, se presentan algunas imágenes relacionadas con las medidas de tendencia central:

Imagen 1

Esta imagen muestra cómo calcular la media, la mediana y la moda para datos agrupados puntualmente.

Imagen 2

Esta imagen muestra un cuestionario sobre las medidas de tendencia central.

Imagen 3

Esta imagen muestra un ejemplo de cómo calcular la mediana para datos agrupados puntualmente.

Imagen 4

Esta imagen muestra un ejemplo de cómo calcular la media, la mediana y la moda utilizando un conjunto de datos.

Imagen 5

Esta imagen muestra un tutorial sobre cómo calcular la media, la mediana y la moda utilizando un conjunto de datos.

Imagen 6

Esta imagen muestra un diagrama que resume las medidas de tendencia central, el rango y el eje medio.

Imagen 7

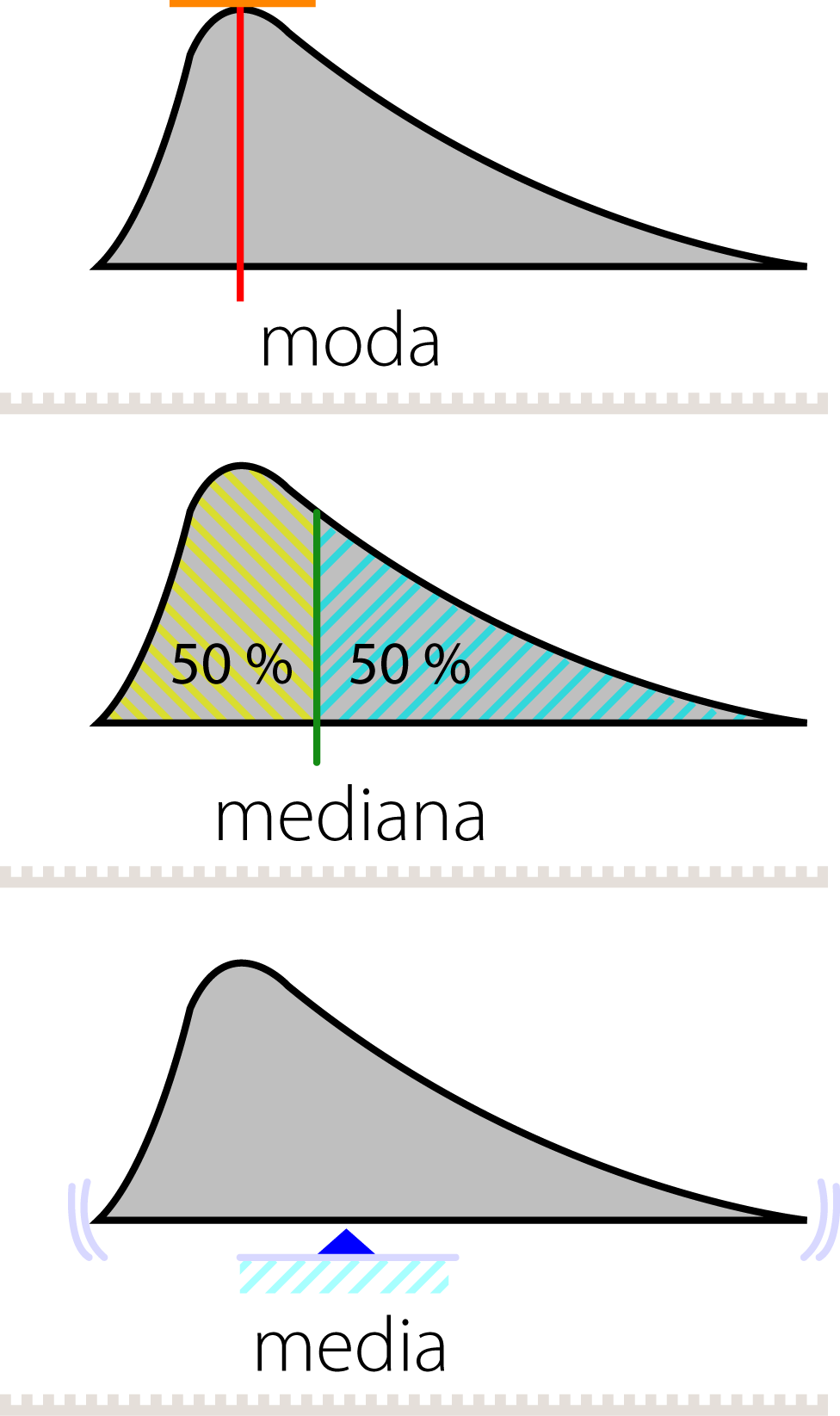
Esta imagen muestra un ejemplo de cómo calcular la media, la mediana y la moda utilizando un conjunto de datos.

Imagen 8

Esta imagen muestra un diagrama que resume las medidas de tendencia central, el rango y el eje medio.

Imagen 9

Esta imagen muestra algunos de los símbolos comunes utilizados para la media, la mediana y la moda.