Medidas De Tendencia Central Media Mediana Y Moda

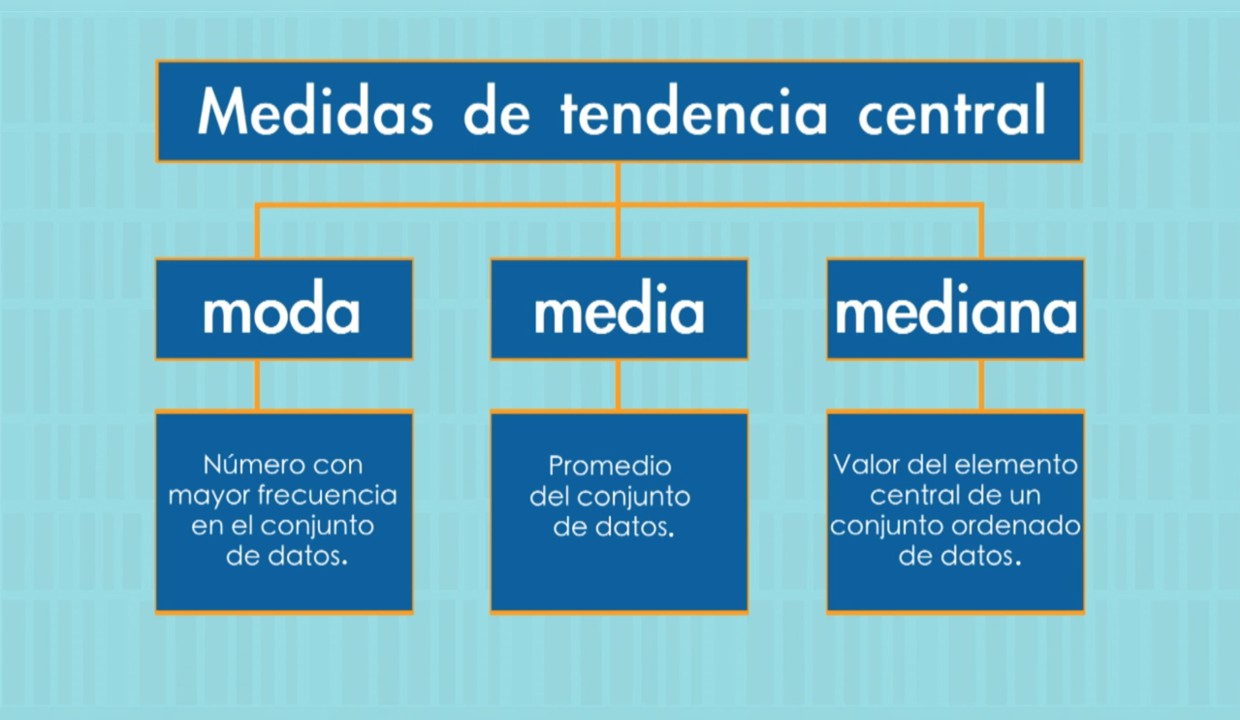
¡Hola amigos! Hoy vamos a hablar de un tema muy interesante y útil en el campo de la estadística: las medidas de tendencia central. Las medidas de tendencia central son una manera de resumir un conjunto de datos en un solo valor, que representa la posición central de los datos. Hay tres medidas de tendencia central principales que vamos a explorar en profundidad: la media, la mediana y la moda. Pero primero, ¿qué es la estadística?

La estadística es una rama de las matemáticas que se enfoca en la recolección, análisis e interpretación de datos. Es una herramienta muy útil en campos como la economía, la medicina, la ingeniería y muchos más. Las medidas de tendencia central son algunas de las herramientas más básicas y importantes en estadística y son utilizadas para encontrar un valor “promedio” o “representativo” en una serie de datos.

La Media

La media, también conocida como promedio, es la medida de tendencia central más comúnmente usada. Para calcular la media, se suman todos los valores en un conjunto de datos y se dividen por la cantidad de valores en el conjunto. Por ejemplo:

Supongamos que tenemos el siguiente conjunto de datos:

5, 10, 15, 20, 25

Para encontrar la media, sumamos todos los valores y dividimos por la cantidad de valores:

(5 + 10 + 15 + 20 + 25) / 5 = 15

Por lo tanto, la media de este conjunto de datos es 15. La media es útil porque toma en cuenta todos los valores en el conjunto de datos y proporciona un indicador sólido del valor promedio en esos datos. Sin embargo, la media puede verse afectada por valores extremadamente altos o bajos en el conjunto de datos.

La Mediana

La mediana es otra medida de tendencia central comúnmente utilizada. La mediana es el valor que se encuentra en el medio de un conjunto de datos cuando se ordenan en orden ascendente o descendente. Si el conjunto de datos tiene una cantidad par de valores, se toma el promedio de los dos valores medios. Por ejemplo:

Supongamos que tenemos el siguiente conjunto de datos:

5, 10, 15, 20, 25

Para encontrar la mediana, primero ordenamos los valores en orden ascendente:

5, 10, 15, 20, 25

El valor medio en este conjunto de datos es 15, por lo que esa es nuestra mediana. Si el conjunto de datos tuviera una cantidad par de valores:

5, 10, 15, 20, 25, 30

El valor medio en este conjunto de datos es el promedio de los dos valores medios, que son 15 y 20:

(15 + 20) / 2 = 17.5

Por lo tanto, la mediana en este conjunto de datos es 17.5. La mediana es útil porque no se ve afectada por valores extremadamente altos o bajos en el conjunto de datos, ya que solo se enfoca en el valor medio.

La Moda

La moda es la tercera medida de tendencia central que vamos a explorar. La moda es el valor que aparece con más frecuencia en un conjunto de datos. Es posible que un conjunto de datos tenga más de una moda si hay dos o más valores que aparecen con la misma frecuencia. Por ejemplo:

Supongamos que tenemos el siguiente conjunto de datos:

5, 10, 10, 15, 20, 20, 20, 25, 25

En este conjunto de datos, el valor que aparece con más frecuencia es 20, por lo que esa es nuestra moda. La moda es útil porque puede proporcionar información sobre los valores más comunes en un conjunto de datos.

Consejos Para Trabajar Con Medidas de Tendencia Central

Aquí hay algunos consejos útiles para trabajar con medidas de tendencia central:

• Comprende el conjunto de datos: Antes de comenzar a calcular cualquier medida de tendencia central, debes entender completamente el conjunto de datos que estás utilizando. Debes saber la cantidad de valores en el conjunto, si hay valores extremadamente altos o bajos que puedan afectar las medidas, y cómo están distribuidos los valores en el conjunto.
• Usa más de una medida de tendencia central: Siempre es útil calcular más de una medida de tendencia central para tener una mejor comprensión de los datos. La media, la mediana y la moda pueden proporcionar información importante sobre un conjunto de datos, pero cada una tiene sus propias limitaciones.
• No te limites a las medidas de tendencia central: Las medidas de tendencia central son importantes, pero no son la única manera de resumir y analizar un conjunto de datos. Es posible que algunas situaciones requieran otros tipos de medidas estadísticas, como la desviación estándar o el coeficiente de variación.

Ideas Prácticas Para Utilizar Medidas de Tendencia Central

Las medidas de tendencia central pueden ser muy útiles en una variedad de situaciones prácticas. Aquí hay algunas ideas:

• En economía: Las medidas de tendencia central pueden ser útiles para analizar los precios de los bienes y servicios en la economía. Por ejemplo, se puede calcular la media o la mediana de los precios de los automóviles vendidos en un país para tener una idea del precio “promedio” de los automóviles.
• En medicina: Las medidas de tendencia central pueden ser útiles para analizar los resultados de pruebas médicas. Por ejemplo, se puede calcular la media de los niveles de colesterol en un grupo de pacientes para determinar el promedio general de los niveles de colesterol.
• En ingeniería: Las medidas de tendencia central pueden ser útiles para analizar la resistencia de los materiales. Por ejemplo, se puede calcular la media de los resultados de pruebas de resistencia del acero para determinar un valor “promedio” de la resistencia del acero.

Cómo Calcular Las Medidas de Tendencia Central

Con los avances en la tecnología y el software estadístico, el cálculo de las medidas de tendencia central se ha vuelto mucho más fácil. Pero para aquellos que aun prefieren no usar programas, aquí hay algunos consejos prácticos para calcular cada medida:

• Media: Calcula la suma de todos los valores en el conjunto de datos y divide por la cantidad de valores.
• Mediana: Ordena los valores en el conjunto de datos y encuentra el valor medio. Si la cantidad de valores es par, encuentra el promedio de los dos valores medios.
• Moda: Encuentra el valor que aparece con más frecuencia en el conjunto de datos. Si hay más de una moda, escribe todas las modas.

En conclusión, las medidas de tendencia central son una herramienta muy útil para resumir y analizar conjuntos de datos en estadística. La media, la mediana y la moda son las medidas de tendencia central más comunes y cada una tiene su propia utilidad y limitaciones. Al comprender completamente el conjunto de datos y utilizar más de una medida de tendencia central, podemos tener una mejor comprensión de los datos y utilizarlos para tomar decisiones informadas y hacer predicciones precisas en una variedad de campos. ¡Gracias por leer y estar atento a más actualizaciones!