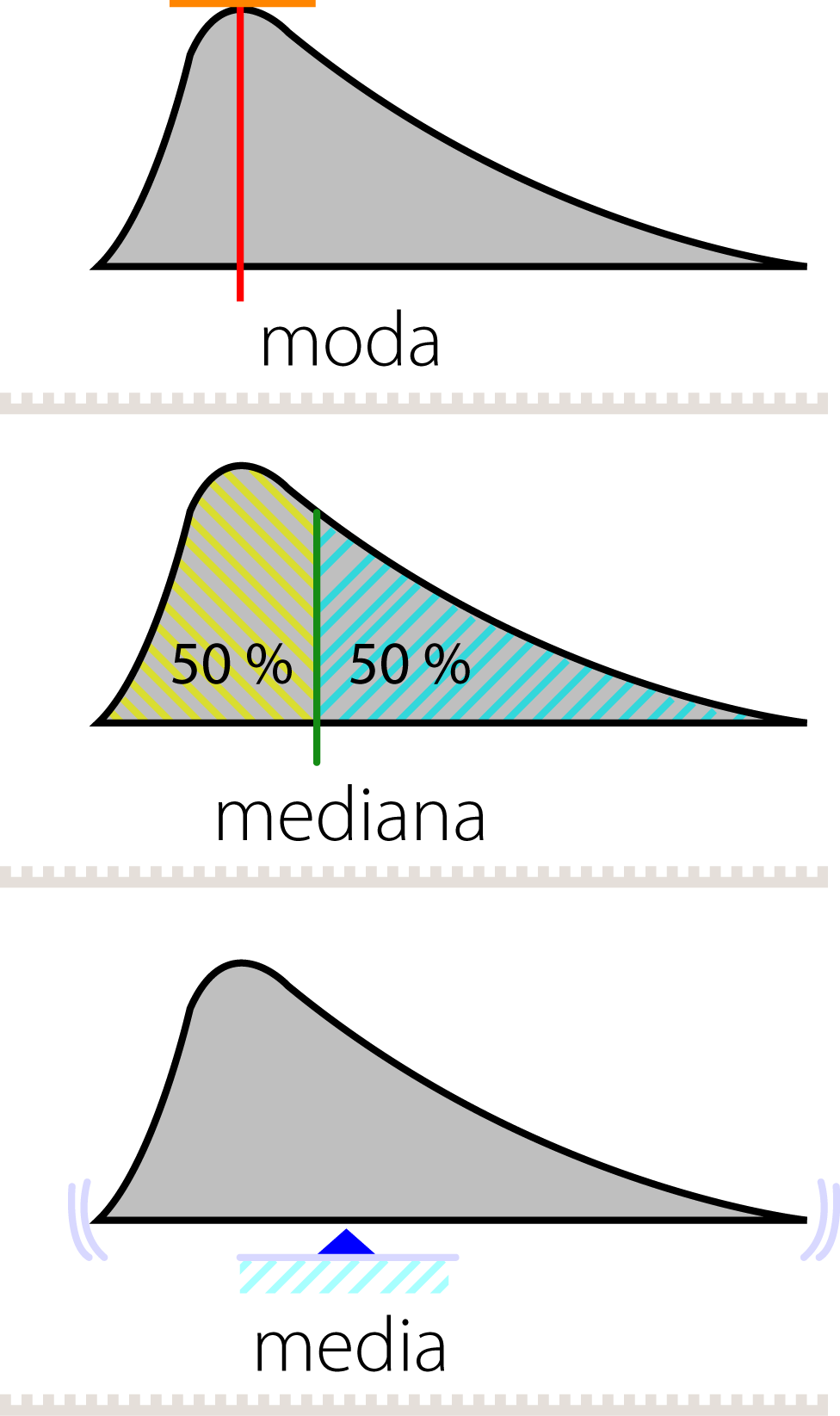
¡Hola a todos! ¿Cómo están hoy? Hoy quiero hablarles sobre algo que puede ser muy útil para entender e interpretar los datos en diferentes ámbitos: las medidas de tendencia central.
Table of Contents
Optimismo Persona australiana voltaje relacion entre media y mediana
Comenzamos con una imagen que muestra la relación entre la media y la mediana en una gráfica de voltaje de una persona australiana. ¿Pero qué es la media y la mediana? La media es el promedio de un conjunto de datos y se obtiene sumando todos los datos y dividiendo entre la cantidad total. Por otro lado, la mediana se encuentra en el valor que se encuentra en el medio de un conjunto de datos ordenados, separando la mitad de los datos más bajos y la mitad de los datos más altos.
En la imagen, podemos ver que la media y la mediana son muy similares, lo que indica que no hay valores atípicos o extremos en los datos. Este es un ejemplo de cómo las medidas de tendencia central pueden ayudarnos a entender y simplificar grandes conjuntos de datos.
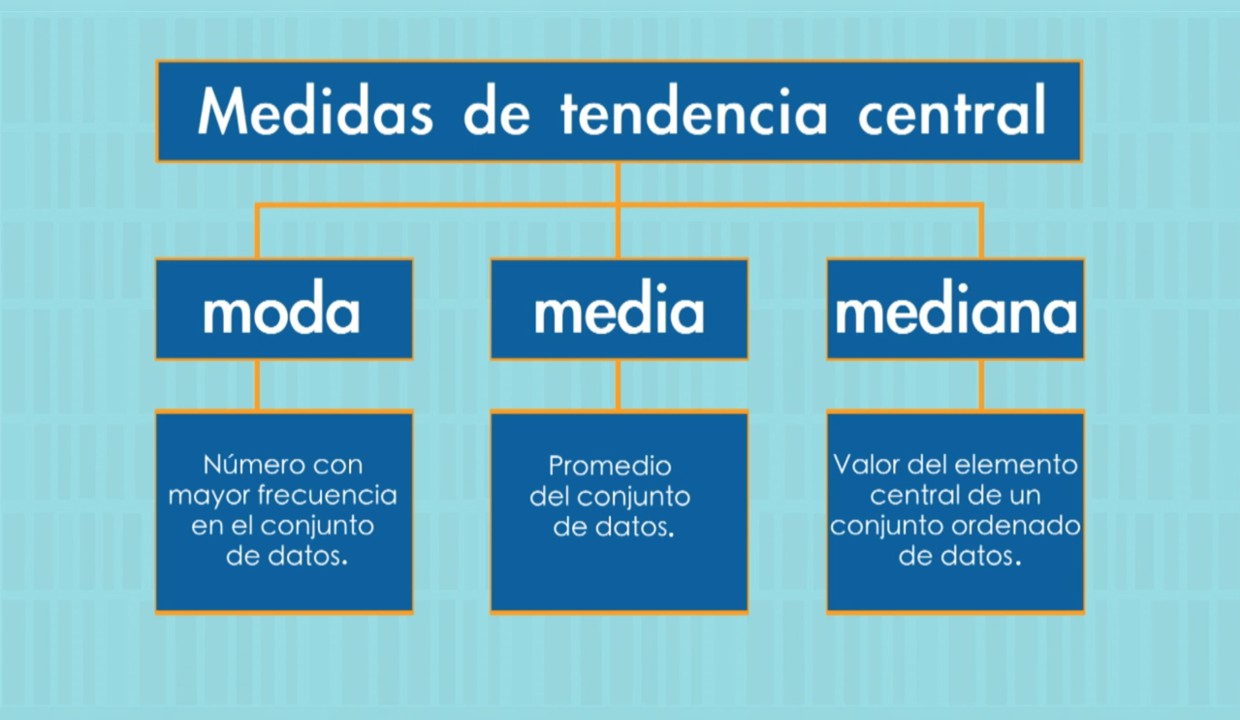
Medidas De Tendencia Central Media Mediana Y Moda Youtube – ThemeLower
En este otro ejemplo, podemos ver cómo se pueden utilizar las medidas de tendencia central en análisis estadísticos. La imagen muestra una captura de pantalla de un video en Youtube que explica las diferencias entre la media, la mediana y la moda y cómo se pueden utilizar en diferentes situaciones.

La media es comúnmente utilizada para representar el promedio de un conjunto de datos, mientras que la mediana se utiliza para encontrar la posición central de un conjunto de datos. La moda, por su parte, indica el valor que aparece con más frecuencia en un conjunto de datos.
Esto es muy útil en diferentes ámbitos, desde los negocios hasta las ciencias sociales. Por ejemplo, si analizamos los precios de productos en el mercado, podemos utilizar la mediana para encontrar un precio justo para el producto, que no sería afectado por valores extremos o atípicos.
Aplicaciones estadísticas del cálculo fraccionario: Promedio y mediana
En esta siguiente imagen, podemos ver cómo las medidas de tendencia central también pueden ser utilizadas en el cálculo fraccionario. La imagen muestra una gráfica y una tabla que utilizan la mediana para encontrar la posición central de un conjunto de datos.

El cálculo fraccionario puede ser aplicado en diferentes situaciones donde los datos son más complejos, como en la economía, las finanzas y la ciencia en general. La mediana, en este caso, es una herramienta muy útil para encontrar el valor central sin verse afectado por valores extremos o atípicos.
Florero Jardines Precaución tendencia central media mediana y moda
Continuamos con una imagen de un florero, que es probablemente lo último que esperaban ver en un artículo sobre estadística. Pero esta imagen es un buen ejemplo de cómo las herramientas de tendencia central pueden ser aplicadas en situaciones cotidianas.
En este caso, podemos utilizar las medidas de tendencia central para analizar la simetría y distribución de los datos. Por ejemplo, si tratamos de hacer un arreglo floral y queremos que tenga una apariencia simétrica, podemos utilizar la mediana para asegurarnos que están las mismas cantidad de flores en cada lado del florero, sin preocuparnos por valores extremos.
MEDIDAS DE TENDENCIA CENTRAL: MEDIA MEDIANA Y MODA – YouTube
En esta otra imagen, tenemos una captura de pantalla de un video de Youtube que explica las medidas de tendencia central de manera clara y sencilla.

Este tipo de recursos en línea pueden ser muy útiles cuando se intenta aprender más sobre estadísticas y matemáticas en general. Los ejemplos y las explicaciones sencillas pueden ayudar a comprender mejor y aplicar estas herramientas en diferentes situaciones cotidianas.
Medidas de tendencia central media, mediana y moda en estadística – YouTube
En este otro video de Youtube, podemos encontrar más información sobre cómo se utilizan las medidas de tendencia central en estadística. La imagen muestra una tabla que relaciona las diferentes situaciones en las que cada medida es más útil.

La media, por ejemplo, es muy útil para encontrar el promedio y la moda es más utilizada cuando buscamos valores extremos. La mediana, por su parte, es efectiva cuando queremos encontrar una posición central en el conjunto de datos.
Medidas de tendencia central en Excel
En esta siguiente imagen, tenemos un ejemplo de cómo se pueden utilizar las medidas de tendencia central en el programa de Excel. La imagen muestra una tabla de datos en la que se han aplicado diferentes fórmulas para encontrar la media, la mediana y la moda.

Esto muestra cómo las medidas de tendencia central pueden ser incorporadas en diferentes programas y herramientas que utilizamos en nuestra vida cotidiana. No se necesita ser un experto en matemáticas para comprender y aplicar estas herramientas.
Seda Destierro cometer diferencia media mediana y moda técnico Capataz
Terminamos con una imagen de una obra de arte, que muestra cómo las medidas de tendencia central también pueden ser utilizadas en el arte y la creatividad. La imagen muestra una pieza de seda titulada “Destierro cometer diferencia media mediana y moda técnico Capataz”.

Esta obra muestra cómo las medidas de tendencia central pueden ser utilizadas para encontrar patrones y simetrías en diferentes formas de arte. En este caso, la pieza de seda muestra un patrón simétrico que se forma utilizando las medidas de tendencia central.
Espero que este artículo haya sido útil para todos ustedes en la comprensión de las medidas de tendencia central. Recuerden, estas herramientas pueden ser aplicadas en diferentes ámbitos y situaciones cotidianas, y no se necesita ser un experto en matemáticas para comprender y utilizar estas herramientas en nuestro día a día.
 Moda y Estilo Las mejores ideas de Estilo de moda
Moda y Estilo Las mejores ideas de Estilo de moda


