
Medidas estadísticas univariantes son una parte crucial del análisis de datos. No importa si eres un estudiante, un profesional o simplemente alguien que está interesado en entender cómo se realizan los estudios estadísticos. La comprensión de las medidas estadísticas univariantes es importante para la toma de decisiones y para la interpretación de datos.
Table of Contents
Medidas de tendencia central
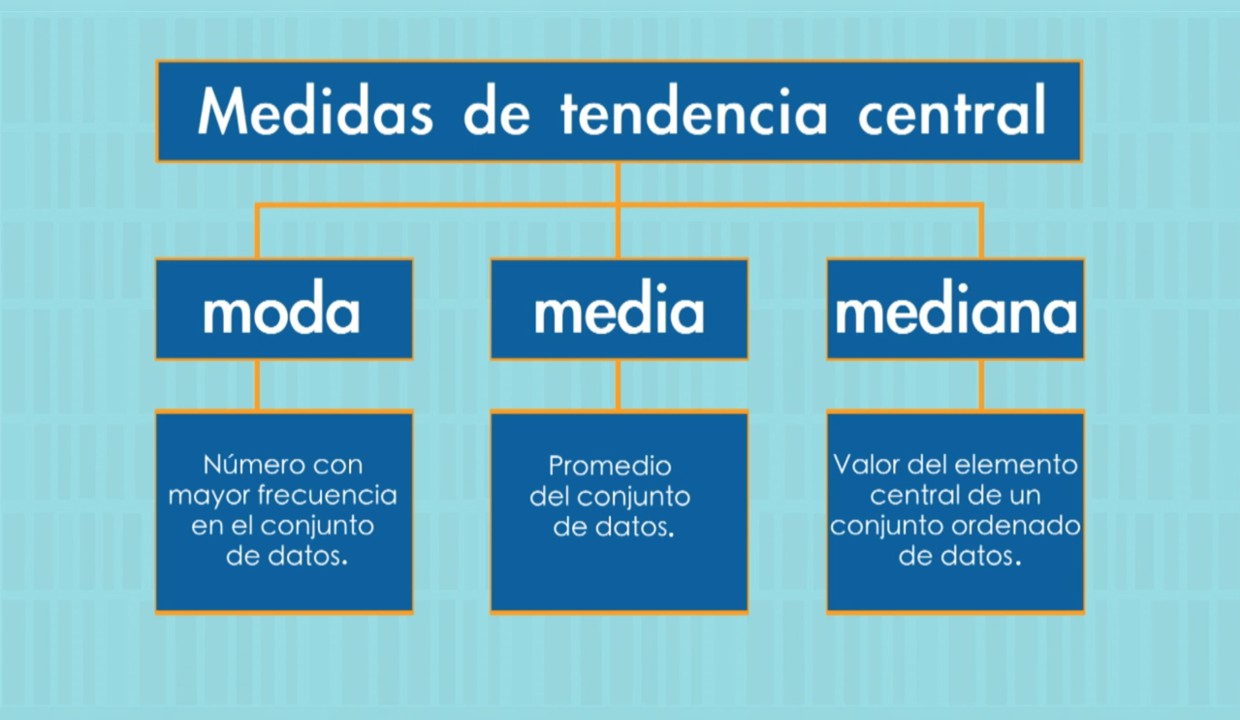
Las medidas de tendencia central son importantes para comprender los patrones de los datos. Esencialmente, te dicen lo que es el centro de los datos. Las tres principales medidas de tendencia central son la media, mediana y moda.
La media es la medida de tendencia central más común. Es la suma de todos los valores dividido por el número de valores en un conjunto de datos. La mediana es el valor medio en un conjunto de datos que se dividen en dos partes iguales, teniendo en cuenta que los datos estén ordenados. La moda es el valor más común en un conjunto de datos.
Para calcular el centro de los datos, asegúrate de ordenarlos de menor a mayor y encontrar su media, mediana y moda. Aprender cómo se calculan estas medidas es una habilidad vital para poder hacer gráficos, estudios y análisis de datos.
Consejos para comprender las medidas de tendencia central
Hay algunos consejos para entender mejor las medidas de tendencia central. En primer lugar, trata de mirar las medidas de tendencia central en el contexto de los datos. Por ejemplo, si estás intentando entender la edad de las personas en una muestra, el promedio de edad es una medida útil de tendencia central.

En segundo lugar, piensa en lo que las medidas representan. La media es sensible a valores atípicos o extremos, mientras que la mediana no lo es tanto. Y la moda puede ser menos útil que la media o la mediana, pero aún así es importante tener en cuenta.
Ideas para utilizar medidas de tendencia central
Las medidas de tendencia central pueden ser muy útiles en ámbitos diversos. En la ciencia, por ejemplo, se utilizan para entender los patrones en los datos y hacer inferencias sobre el universo. En la industria, se utilizan para calcular la rentabilidad y los costes. Y en la vida diaria, se utilizan para hacer presupuestos y tomar decisiones.

Las medidas de tendencia central también son útiles en la toma de decisiones y para la interpretación de datos. Por ejemplo, si estás interesado en comprar una casa, es posible que desees saber cuál es el promedio de precios de las casas en tu ciudad o estado. Y si estás preocupado por la inflación o el salario mínimo, puedes utilizar las medidas de tendencia central para analizar los datos relevantes y tomar decisiones informadas.
Comprender la relación entre la media y la mediana
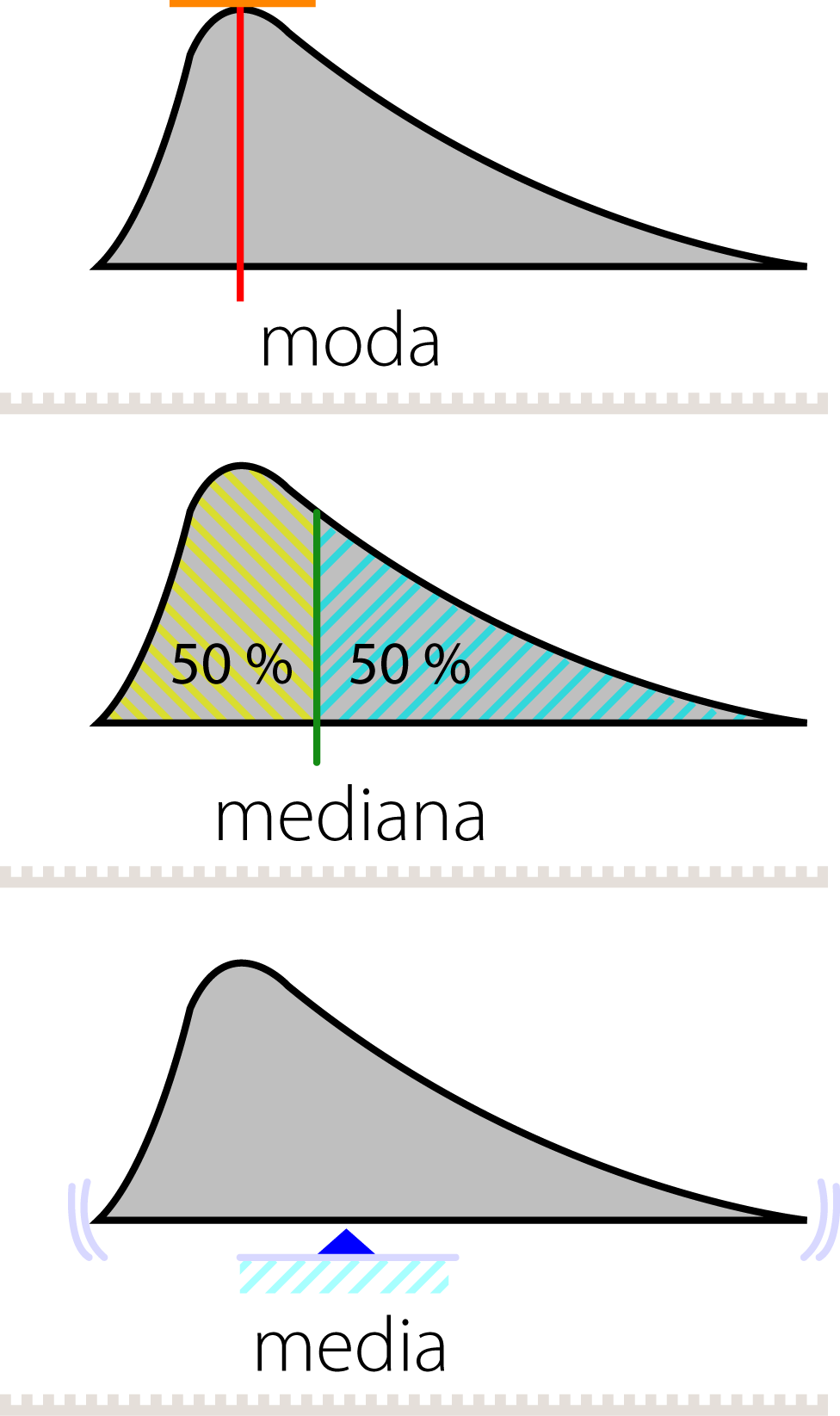
La relación entre la media y la mediana es importante para entender la forma en que se distribuyen los datos. En general, si los datos están distribuidos de manera uniforme, la media y la mediana serán iguales. Si la distribución de los datos no es uniforme, la media y la mediana serán diferentes.
Un ejemplo de esto es el salario. Si observamos una muestra de salarios, es común que haya salarios muy bajos y salarios muy altos. Esto significa que la distribución no es uniforme. En este caso, la media será más alta que la mediana porque los salarios muy altos inflan el resultado. Por lo tanto, la elección de una medida de tendencia central dependerá del contexto y de los datos disponibles.
Usando las medidas de tendencia central para tomar decisiones informadas
Las medidas de tendencia central son muy útiles para tomar decisiones informadas en muchas áreas de la vida. En los negocios, por ejemplo, las medidas de tendencia central como la media, la mediana y la moda se utilizan para hacer presupuestos y proyecciones. En la ciencia, se utilizan para entender patrones y relaciones en los datos.
Para utilizar las medidas de tendencia central correctamente, es importante entender su contexto y la relación que tienen con los datos. Por ejemplo, si estás estudiando la obesidad, es útil entender la diferencia entre la media y la mediana de los pesos.
Cómo utilizar las medidas de tendencia central en un estudio estadístico
Si estás haciendo un estudio estadístico, es importante utilizar las medidas de tendencia central correctamente. Primero, determina la medida de tendencia central que mejor se adapte a tus datos. En segundo lugar, utiliza gráficos para visualizar tus conclusiones. Y en tercer lugar, asegúrate de interpretar tus resultados cuidadosamente para hacer inferencias apropiadas.

Las medidas de tendencia central son una herramienta poderosa en el análisis de datos. Aprender a usarlas correctamente puede ayudarte en tu vida cotidiana y en tu carrera. Y recuerda, siempre revisa tus resultados y sé cauteloso al hacer inferencias basadas en los datos.
 Moda y Estilo Las mejores ideas de Estilo de moda
Moda y Estilo Las mejores ideas de Estilo de moda


