
¡Hola amigos! ¿Cómo están hoy? Hoy quiero hablarles sobre algo muy importante en estadística: las medidas de tendencia central. Puede sonar un poco técnico, pero en realidad es bastante simple de entender. Aquí les presento algunas imágenes que les ayudarán a comprender mejor este concepto:
Table of Contents
Mapa Conceptual De Medidas De Tendencia Central Necto Images
En esta imagen podemos ver un mapa conceptual de las medidas de tendencia central. Como podemos ver, hay tres medidas principales: la media, la mediana y la moda. Estas medidas nos ayudan a entender cuál es el valor central de un conjunto de datos.
La media es la suma de todos los valores dividida entre el número de valores que tenemos. Por ejemplo, si tenemos los siguientes datos: 2, 5, 8, 10, la media sería (2+5+8+10)/4 = 6.25.
La mediana es el valor central de un conjunto de datos ordenados. Para encontrar la mediana, tenemos que ordenar los datos de menor a mayor o de mayor a menor y buscar el valor que se encuentra en el medio de la lista. Si hay un número par de valores, se toma la media de los dos valores centrales. Por ejemplo, si tenemos los siguientes datos: 2, 5, 8, 10, la mediana sería 6.5.
La moda es el valor que se repite con más frecuencia en un conjunto de datos. Por ejemplo, si tenemos los siguientes datos: 2, 5, 8, 8, 10, la moda sería 8.
Aplicaciones estadísticas del cálculo fraccionario: Promedio y mediana
Esta imagen nos muestra cómo se pueden aplicar las medidas de tendencia central en el cálculo fraccionario. Aquí podemos ver cómo se calcula el promedio y la mediana de un conjunto de datos fraccionarios. Es importante recordar que estos cálculos son iguales a los realizados con números enteros.

Por ejemplo, si tenemos los siguientes datos fraccionarios: 1/2, 3/4, 5/6, 7/8, podemos calcular la media sumando los valores y dividiendo entre el número de valores: (1/2 + 3/4 + 5/6 + 7/8)/4 = 15/16. La mediana sería el valor que se encuentra en el medio de la lista ordenada, que en este caso sería 5/6.
Cómo calcular medidas de tendencia central para datos estadísticos
En esta imagen podemos ver los pasos para calcular las medidas de tendencia central en datos estadísticos. Es importante seguir estos pasos para obtener resultados precisos.
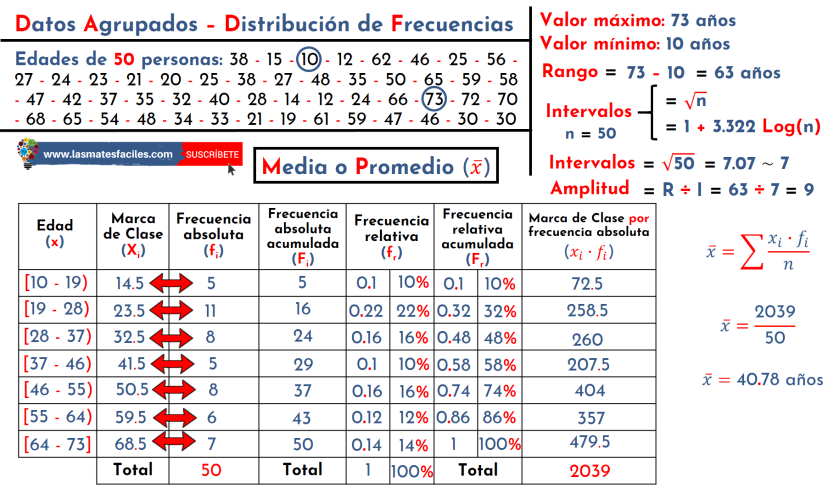
En primer lugar, tenemos que reunir todos los datos. Luego, podemos calcular la media sumando todos los valores y dividiendo entre el número de valores. La mediana se calcula ordenando los datos y buscando el valor que se encuentra en el medio de la lista. La moda se obtiene buscando el valor que se repite con más frecuencia.
MEDIA MODA MEDIANA EJERCICIOS RESUELTOS
Esta imagen nos muestra algunos ejercicios resueltos para calcular la media, la moda y la mediana en un conjunto de datos. Es importante practicar este tipo de ejercicios para comprender mejor el concepto.

Por ejemplo, si tenemos los siguientes datos: 2, 5, 8, 10, podemos calcular la media sumando todos los valores y dividiendo entre el número de valores: (2+5+8+10)/4 = 6.25. La mediana sería 6.5, ya que es el valor que se encuentra en el medio de la lista ordenada. La moda sería 8, ya que es el valor que se repite con más frecuencia.
Media Mediana Y Moda Early Math Quiz Quizizz – Mobile Legends
Esta imagen nos muestra cómo se pueden aplicar las medidas de tendencia central en la enseñanza de las matemáticas. Utilizar juegos y actividades interactivas puede ayudar a los estudiantes a comprender mejor estos conceptos.

Por ejemplo, se puede utilizar un juego como Quizizz para que los estudiantes practiquen el cálculo de la media, la mediana y la moda en un ambiente divertido y desafiante.
Medidas de tendencia central ~ Matemáticas y Estadística
Esta imagen nos muestra las medidas de tendencia central en un contexto más amplio de las matemáticas y la estadística. Es importante comprender la relación entre estos conceptos para entender mejor cómo se pueden aplicar en diferentes campos.

Las medidas de tendencia central se utilizan en muchos campos diferentes, como la economía, la salud y la educación. Por ejemplo, en economía se pueden utilizar estas medidas para comprender las tendencias del mercado y tomar decisiones informadas. En salud, se pueden utilizar para analizar datos de ensayos clínicos y estudios epidemiológicos. En educación, se pueden utilizar para evaluar el rendimiento de los estudiantes y tomar decisiones sobre el plan de estudio.
Medidas de tendencia central media, mediana y moda en estadística – YouTube
Esta imagen nos muestra un video en YouTube que explica cómo se pueden calcular las medidas de tendencia central en estadística. Ver videos educativos puede ser una forma efectiva de aprender sobre estos conceptos.

Como podemos ver, existen muchas maneras de aprender sobre las medidas de tendencia central. Lo importante es tener una comprensión clara de estos conceptos y saber cómo aplicarlos en diferentes situaciones.
Espero que esta información les haya sido útil. No duden en dejar sus comentarios y preguntas abajo. ¡Nos vemos pronto!
 Moda y Estilo Las mejores ideas de Estilo de moda
Moda y Estilo Las mejores ideas de Estilo de moda


