
Las medidas de tendencia central son herramientas estadísticas que nos permiten conocer cómo se distribuyen los datos de un conjunto de valores. Cuando trabajamos con datos, es muy frecuente que nos interese tener una idea de cuál es el valor que se considera central o típico. Si estamos hablando de notas, por ejemplo, puede que queramos saber cuál es la nota media o promedio de un grupo de estudiantes.
Table of Contents
¿Qué son las medidas de tendencia central?
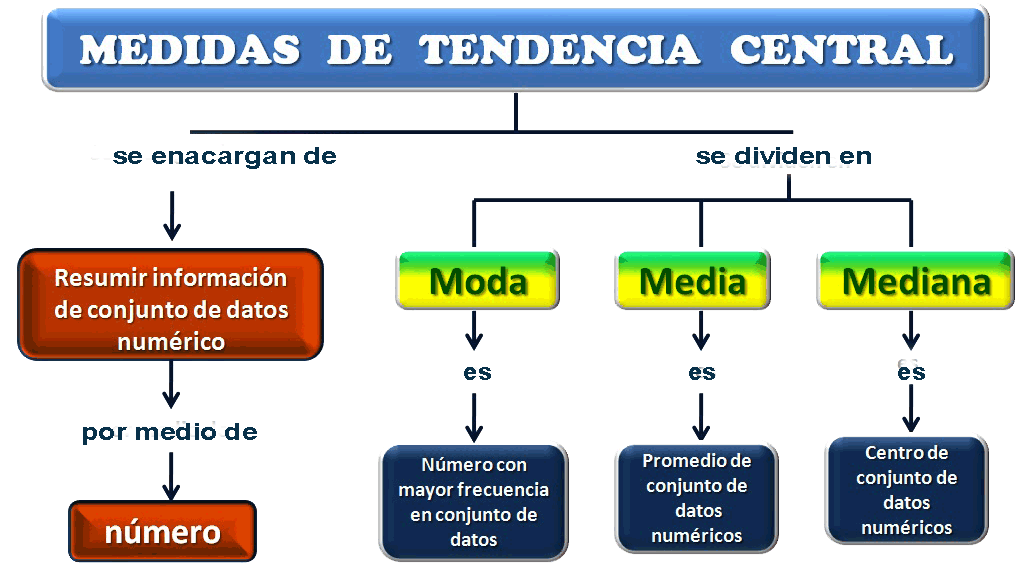
Las medidas de tendencia central son estadísticas que reflejan la posición de un conjunto de datos. Sirven para sintetizar la información obtenida a partir de un conjunto de datos y para representar el “valor central” o “típico” de dichos datos.
Media aritmética
La media aritmética es la medida de tendencia central más conocida y utilizada. Se obtiene sumando todos los valores y dividiendo entre el número de elementos. La media es muy sensible a los valores extremos de un conjunto de datos, por lo que puede no ser la mejor medida de uso para todos los casos.
Mediana
La mediana es el valor que separa un conjunto de datos ordenados en dos partes iguales (50% de los datos están por encima y 50% de los datos están por debajo). La mediana es menos sensible a los valores extremos que la media, lo que la convierte en una buena medida de tendencia central para conjuntos de datos con valores extremos o asimétricos.

Moda
La moda es el valor que aparece con mayor frecuencia en el conjunto de datos. Si los datos están distribuidos de manera simétrica, la moda será igual a la media y la mediana. Si la distribución no es simétrica, la moda puede ser una buena medida de tendencia central para reflejar la parte más importante de los datos.

Consejos para el uso de las medidas de tendencia central
Es importante tener en cuenta algunas consideraciones al utilizar las medidas de tendencia central:
- Antes de elegir una medida de tendencia central, debemos analizar la distribución de los datos para entender si los valores son simétricos o asimétricos. Si los valores son asimétricos, la mediana puede ser una mejor medida que la media.
- Es importante tener en cuenta la dispersión de los datos. No es lo mismo trabajar con un conjunto de datos con poca dispersión – en ese caso, las tres medidas pueden ser adecuadas – que trabajar con datos disgregados. Si la dispersión es alta, la media puede no ser una buena medida de tendencia central.
- Las medidas de tendencia central no son infalibles. Sirven para tener una idea general de la distribución de los datos, pero no reflejan todas las variaciones y características de los mismos. Hay otros indicadores estadísticos que nos permiten profundizar en el análisis.
Ideas para el uso de las medidas de tendencia central
La mayoría de las personas asocian el uso de las medidas de tendencia central a la estadística y las matemáticas, pero en realidad están presentes en distintas áreas de la sociedad:
- En la economía, las medidas de tendencia central se utilizan para analizar variables como la inflación. La tasa de inflación es una medida que sirve para medir el aumento generalizado de los precios de los bienes y servicios en un período de tiempo determinado. La tasa de inflación se calcula utilizando la media de los precios de un conjunto de bienes y servicios.
- En el deporte, las medidas de tendencia central se utilizan para analizar el rendimiento de los equipos. En el fútbol, por ejemplo, podemos analizar la media de goles por partido de un equipo, la mediana de las posesiones de balón o la moda de las faltas cometidas.
- En la ecología, las medidas de tendencia central se utilizan para analizar la distribución de las especies en una población. La moda refleja la especie más común de la población, mientras que la mediana refleja la especie que está presente en el punto medio de la población.
- En la sociología, las medidas de tendencia central se utilizan para analizar la distribución de los ingresos de una población. La media de los ingresos es una medida que refleja el ingreso promedio de la población, mientras que la mediana refleja el ingreso que está en el punto medio entre el mayor y el menor ingreso.
¿Cómo utilizar las medidas de tendencia central?
Para utilizar las medidas de tendencia central, es necesario seguir los siguientes pasos:
- Identificar qué variable se quiere analizar y recolectar los datos.
- Organizar los datos en una tabla.
- Calcular las medidas de tendencia central para los datos.
- Analizar las medidas y tomar conclusiones.
En resumen, las medidas de tendencia central son herramientas útiles para analizar conjuntos de datos y obtener información relevante. Es importante tener un conocimiento básico de estas medidas y saber aplicarlas adecuadamente en cada situación.
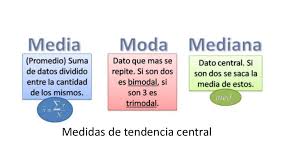
Recuerda siempre tener en cuenta la distribución de los datos y la dispersión de los mismos para elegir la mejor medida de tendencia central. ¡Anímate a utilizarlas y sácale el máximo provecho a tus análisis estadísticos!
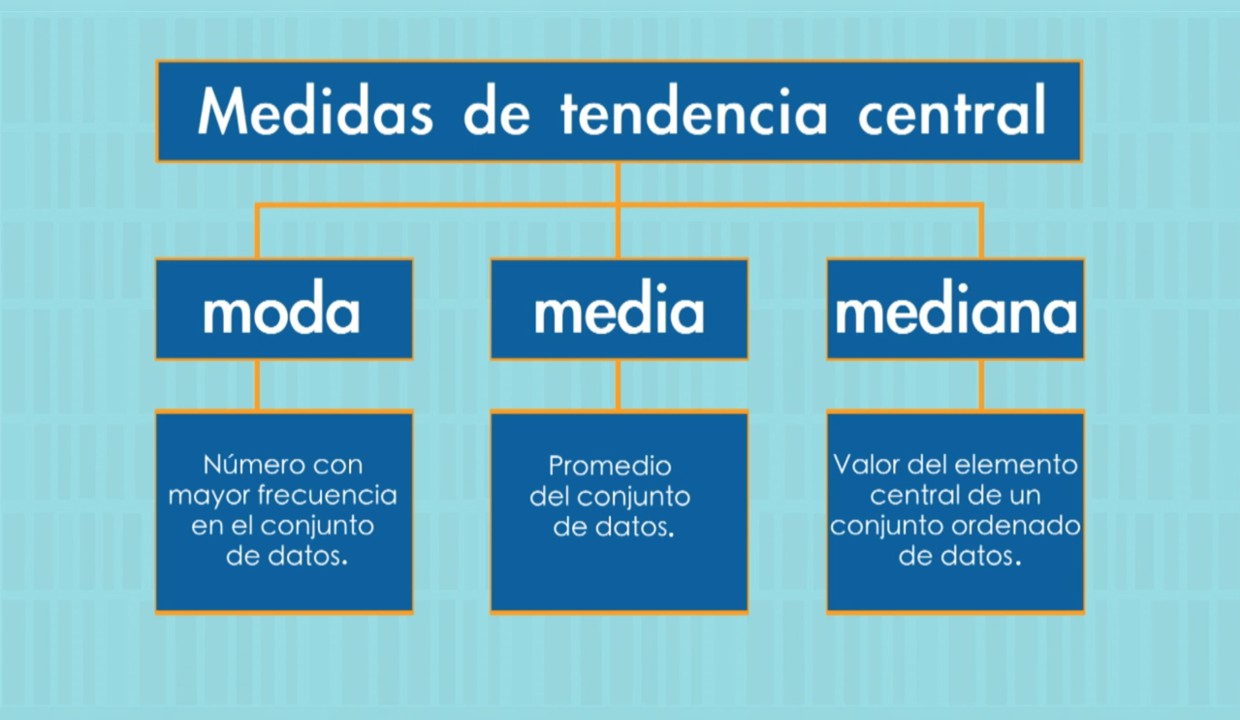
Cómo no equivocarse al utilizar las medidas de tendencia central
Finalmente, hay algunos errores comunes que debemos evitar al utilizar las medidas de tendencia central:
- No considerar la distribución de los datos: para elegir la mejor medida de tendencia central, es esencial analizar la distribución de los datos. Si los datos son asimétricos o tienen valores extremos, la mediana o la moda pueden ser mejores medidas que la media.
- No considerar la dispersión de los datos: la dispersión de los datos es importante porque puede afectar la elección de la medida de tendencia central. Si los datos están muy dispersos, la media puede no ser una buena medida de tendencia central.
- No tener en cuenta otros indicadores estadísticos: aunque las medidas de tendencia central son muy útiles, no son infalibles. Es importante tener en cuenta otros indicadores estadísticos que permitan profundizar en el análisis de los datos.

Para evitar estos errores, es fundamental tener un conocimiento sólido de las medidas de tendencia central y saber cómo aplicarlas adecuadamente en cada situación. ¡No te confíes y sigue aprendiendo!
Conclusión
Las medidas de tendencia central son estadísticas que nos permiten obtener información relevante y útil a partir de conjuntos de datos. La media, la mediana y la moda son las medidas más conocidas y utilizadas, pero es importante tener en cuenta la distribución y la dispersión de los datos para elegir la mejor medida de tendencia central en cada caso.
Además, las medidas de tendencia central están presentes en distintas áreas de la sociedad, desde la economía y el deporte hasta la ecología y la sociología. Aprender a utilizar las medidas de tendencia central nos permite analizar y tomar decisiones más informadas en nuestra vida diaria.
 Moda y Estilo Las mejores ideas de Estilo de moda
Moda y Estilo Las mejores ideas de Estilo de moda

