
¡Hola a todos y todas! Hoy les traigo una súper información sobre uno de los temas más importantes y útiles en las matemáticas: las medidas de tendencia central. Como saben, estas medidas nos permiten obtener información valiosa sobre un conjunto de datos, identificando en ellos una “tendencia” a agruparse alrededor de ciertos valores centrales. ¡Y son muchísimas las aplicaciones de estas medidas en distintos campos, desde la estadística hasta la economía, pasando por la física, la medicina y el marketing!
Pero antes de profundizar en los distintos tipos de medidas de tendencia central, recordemos que hay tres medidas básicas que todos debemos conocer:
– La media aritmética, que se obtiene sumando todos los valores y dividiendo por la cantidad de ellos.
– La mediana, que es el valor que divide al conjunto de datos en dos partes iguales.
– La moda, que es el valor que aparece con mayor frecuencia en el conjunto de datos.
Estas tres medidas son las más comunes y sencillas de calcular, pero no siempre son suficientes para obtener una información completa sobre un conjunto de datos. Por eso, existen otras medidas más avanzadas que permiten obtener una visión más precisa y detallada.
En las siguientes secciones, les mostraré algunas imágenes y les explicaré cómo funcionan estas medidas de tendencia central en cada caso. ¡Comencemos!
Table of Contents
Media ponderada
La media ponderada es una variante de la media aritmética que toma en cuenta el peso de cada valor en el conjunto de datos. En otras palabras, se da mayor importancia a los valores que tienen un impacto mayor en el resultado final. Por ejemplo, si medimos el promedio de las notas de un curso, podríamos asignar un peso mayor a las notas de los exámenes finales que a las notas de los controles semanales. Así, si un alumno tiene un buen desempeño en el examen final, su nota tendrá un impacto mayor en el promedio final del curso.
Consejo: Si quieres calcular la media ponderada de un conjunto de datos, multiplica cada valor por su respectivo peso y luego divide la suma de todos los productos por la suma de los pesos.
Mediana ponderada
La mediana ponderada es una variante de la mediana que toma en cuenta el peso de cada valor en el conjunto de datos. Esta medida es útil cuando tenemos valores extremos que podrían distorsionar el resultado final si solo calculáramos la mediana simple. Por ejemplo, si medimos los ingresos de un grupo de personas, podríamos asignar un peso mayor a los ingresos de la mayoría de las personas que a los ingresos de una minoría muy rica. Así, la mediana ponderada nos dará una idea más precisa de la situación económica del grupo en cuestión.
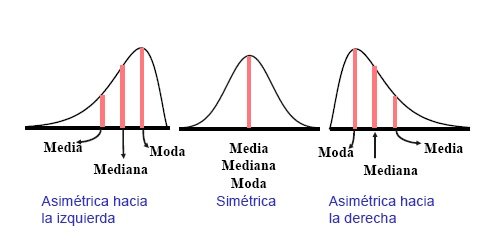
Consejo: Si quieres calcular la mediana ponderada de un conjunto de datos, ordena los valores en forma descendente según su peso y luego encuentra el valor que divide al conjunto de datos en dos partes iguales. En caso de que los pesos no estén ordenados, primero deberás ordenarlos en forma descendente y luego encontrar la mediana simple de los valores correspondientes.
Media geométrica
La media geométrica es una variante de la media aritmética que se utiliza para calcular tasas de crecimiento o decremento. Por ejemplo, si queremos saber cuál fue la tasa de crecimiento promedio de una empresa durante un período determinado, la media geométrica nos dará una respuesta más precisa que la media aritmética. ¿Por qué? Porque la media geométrica considera los cambios porcentuales de los valores, mientras que la media aritmética solo considera las diferencias absolutas.

Consejo: Si quieres calcular la media geométrica de un conjunto de datos, multiplica los valores entre sí y luego encuentra la raíz enésima del producto, donde n es la cantidad de valores.
Media armónica
La media armónica es otra variante de la media aritmética que se utiliza cuando los valores corresponden a razones o proporciones inversas. Por ejemplo, si queremos saber cuál fue la velocidad promedio de un automóvil durante un trayecto determinado, la media armónica nos dará una respuesta más precisa que la media aritmética. ¿Por qué? Porque la media armónica considera el tiempo que se tarda en recorrer cada tramo, mientras que la media aritmética solo considera la distancia total recorrida y el tiempo total empleado.

Consejo: Si quieres calcular la media armónica de un conjunto de datos, divide la cantidad de valores por la suma de las inversiones de cada valor, donde la inversión de un valor es igual a 1 dividido por ese valor.
Moda ponderada
La moda ponderada es una variante de la moda que se utiliza cuando hay valores repetidos en el conjunto de datos y cada valor tiene un peso distinto. Por ejemplo, si queremos saber cuál fue la prenda de vestir preferida de un grupo de personas, podríamos asignar un peso mayor a las opiniones de ciertos miembros del grupo que a las opiniones de otros miembros. Así, la moda ponderada nos dará una respuesta más precisa de la prenda de vestir preferida por el grupo en cuestión.

Consejo: Si quieres calcular la moda ponderada de un conjunto de datos, suma los pesos de cada valor y encuentra el valor con el mayor peso. Si hay dos o más valores con el mayor peso, elige aquel que corresponde al valor que aparece primero en el conjunto de datos.
¡Y estas son solo algunas de las medidas de tendencia central que podemos utilizar para analizar distintos tipos de conjuntos de datos! Como pueden ver, cada medida tiene sus propias características y aplicaciones, por lo que es importante conocerlas todas para poder elegir la más adecuada en cada caso.
Como aplicar estas medidas en la vida cotidiana
Les estarán preguntando como aplicar estos conocimientos en nuestra vida cotidiana, para esto les daré algunas ideas para hacerlo, por ejemplo:
Si estamos en una situación de crisis económica y nos preguntamos cómo afectará a nuestras finanzas personales, podríamos utilizar la media geométrica para calcular la tasa de inflación o devaluación promedio de varios productos o servicios que consumimos a diario, como el pan, la leche, el combustible y el transporte público. De esta manera, podríamos tener una idea más clara de cuánto deberíamos ajustar nuestro presupuesto para afrontar la situación.
Si somos estudiantes o docentes y queremos evaluar el desempeño de un grupo de alumnos en una asignatura, podríamos utilizar la media ponderada para asignar un mayor peso a las notas de los exámenes parciales o finales que a las notas de los trabajos prácticos o los controles de lectura. De esta manera, podríamos obtener un promedio ponderado que refleje de manera más precisa el nivel de conocimientos del grupo.
Si somos deportistas o entrenadores y queremos mejorar nuestro rendimiento físico, podríamos utilizar la media aritmética para calcular el promedio de nuestras marcas o tiempos en distintas pruebas físicas, como el salto en largo, la carrera de velocidad y el lanzamiento de peso. De esta manera, podríamos establecer objetivos realistas y monitorear nuestro progreso a lo largo del tiempo.
En resumen, las medidas de tendencia central son una herramienta indispensable para analizar y comprender distintos tipos de conjuntos de datos, desde los más simples hasta los más complejos. ¡Así que no duden en aplicarlas en su vida diaria y sacarles el máximo provecho!
 Moda y Estilo Las mejores ideas de Estilo de moda
Moda y Estilo Las mejores ideas de Estilo de moda


