
En el mundo del análisis de datos, las medidas de tendencia central son conceptos fundamentales que todo profesional debe conocer. Se consideran como un conjunto de herramientas estadísticas que permiten determinar la ubicación central de un conjunto de datos. En este artículo, exploraremos las medidas de tendencia central más comunes: la media, la mediana y la moda. Además, brindaremos consejos útiles sobre cómo utilizar estas medidas en cualquier análisis de datos.
Table of Contents
La Media
La media, también conocida como promedio, es la medida más común de tendencia central. Esta medida se determina al sumar todos los valores en un conjunto de datos y dividirlos por el número total de elementos en el conjunto. La fórmula para calcular la media es:
La media se utiliza comúnmente para resumir datos numéricos. Por ejemplo, si tenemos el conjunto de datos [4, 5, 6, 7, 8], podemos determinar la media como:

La media es una medida de tendencia central bastante robusta, ya que tiende a ser bastante resistente a valores atípicos en un conjunto de datos. Sin embargo, si hay valores extremadamente grandes o pequeños en el conjunto de datos, la media puede ser engañosa.
La Mediana
La mediana es otra medida común de tendencia central. Para determinar la mediana, se ordenan los elementos de un conjunto de datos en orden ascendente o descendente y se selecciona el valor central. Si el conjunto de datos tiene un número par de elementos, se toma el promedio de los dos valores centrales. La fórmula para calcular la mediana es:

La mediana se utiliza comúnmente para resumir datos ordinales o que tienen un rango más amplio de valores. Por ejemplo, si tenemos el conjunto de datos [4, 5, 6, 7, 8, 9], podemos determinar la mediana como:

La mediana es más resistente a valores atípicos que la media. Esta medida es especialmente útil cuando los datos tienen una distribución no normal y hay valores extremos presentes.
La Moda
La moda es otra medida común de tendencia central. La moda se determina al encontrar el valor que ocurre con más frecuencia en un conjunto de datos. Un conjunto de datos puede tener una moda (unimodal) o varias modas (bimodal, trimodal, etc.). La moda se utiliza comúnmente para resumir datos categóricos. Por ejemplo, si tenemos el conjunto de datos [“manzana”, “naranja”, “naranja”], podemos determinar la moda como “naranja”.

La moda es una medida de tendencia central útil para describir datos discretos, pero no es muy resistente a valores atípicos.
Consejos para utilizar las medidas de tendencia central
Aquí se muestran algunos consejos prácticos para usar las medidas de tendencia central en el análisis de datos:
Consejo #1: Analiza los valores extremos
Antes de elegir una medida de tendencia central, es importante analizar los valores extremos en un conjunto de datos. Los valores atípicos pueden afectar drásticamente la media y hacer que sea una medida inadecuada. La mediana y la moda son más robustas y pueden proporcionar una mejor descripción de los datos en presencia de valores extremos.
Consejo #2: Elije la medida adecuada para el tipo de datos
La media es una buena medida de tendencia central para datos numéricos, mientras que la moda es mejor para datos categóricos. La mediana es útil para datos que tienen valores atípicos o datos que están en un orden que no permite utilizar la media.
Consejo #3: Calcula varias medidas de tendencia central
Es interesante calcular varias medidas de tendencia central para obtener una imagen completa de los datos. Comparar la media, mediana y moda puede ayudar a identificar si los valores en un conjunto de datos están afectados por valores extremos. En los casos en que la media y la mediana no son iguales, es posible que los datos tengan una distribución sesgada.
Ideas clave para recordar
- Las medidas de tendencia central son herramientas estadísticas útiles para resumir conjuntos de datos.
- Las medidas de tendencia central más comunes incluyen la media, mediana y moda.
- La media es la medida de tendencia central más común y se utiliza para resumir datos numéricos.
- La mediana es resistente a los valores atípicos, por lo que suele ser el preferido para resumir datos que presentan valores extremos.
- La moda se utiliza para resumir datos categóricos y es útil cuando las variables tienen pocas categorías.
- Es importante elegir la medida de tendencia central adecuada para el tipo de datos analizados.
Cómo usar las medidas de tendencia central en el análisis de datos
Las medidas de tendencia central son una herramienta común en el análisis de datos. Se utilizan para resumir conjuntos de datos y proporcionar información valiosa sobre la distribución de los datos. Aquí hay un ejemplo de cómo utilizar las medidas de tendencia central en el análisis de datos:
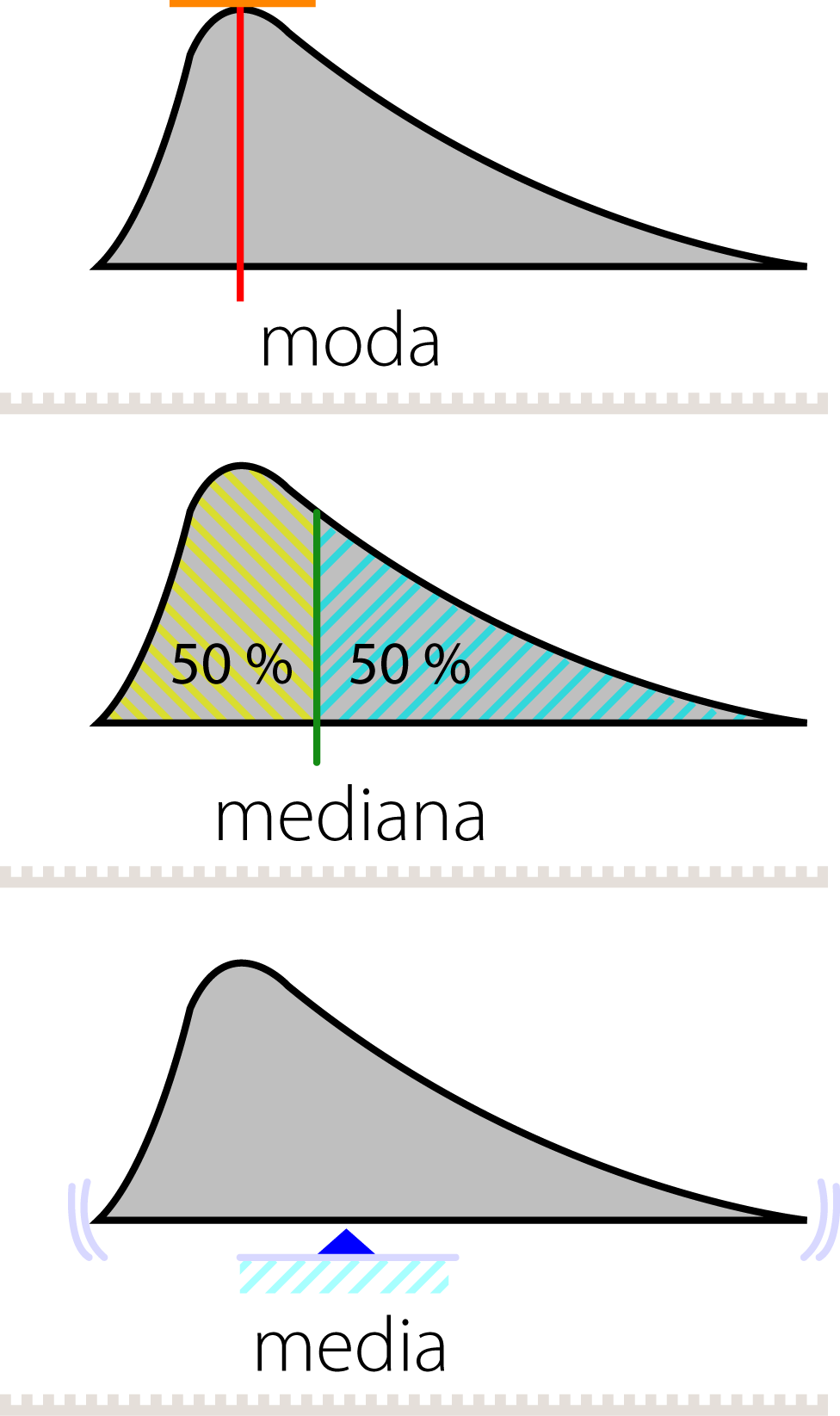
En este ejemplo, analizamos el precio de un conjunto de casa en una calle determinada. Calculamos la media, mediana y moda del conjunto de datos de precios. La media se utilizó para obtener una idea general del precio de las casas en la calle, la mediana se utilizó para determinar un precio medio y la moda se utilizó para identificar el precio más común en la calle. Al analizar estas medidas de tendencia central juntas, podemos obtener una visión completa del panorama de precios en la calle y tomar decisiones informadas en función de esta información.
En conclusión, las medidas de tendencia central son herramientas esenciales para cualquier profesional que trabaje con análisis de datos. Saber cómo utilizar estas medidas es crucial para realizar análisis precisos y tomar decisiones informadas. Con la información presentada en este artículo, esperamos que estés mejor preparado para utilizar estas medidas en tus propios proyectos.
 Moda y Estilo Las mejores ideas de Estilo de moda
Moda y Estilo Las mejores ideas de Estilo de moda


