Medidas De Tendencia Central Moda Mediana Y Promedio

Hoy quiero compartir con todos ustedes un tema muy importante en el ámbito de las matemáticas y la estadística: las medidas de tendencia central. En resumen, estas medidas nos permiten conocer la ubicación central de un conjunto de datos. Pero, ¿cómo se calculan y para qué sirven? ¡Sigue leyendo y descubre más sobre este interesante tema!

Medidas de tendencia central

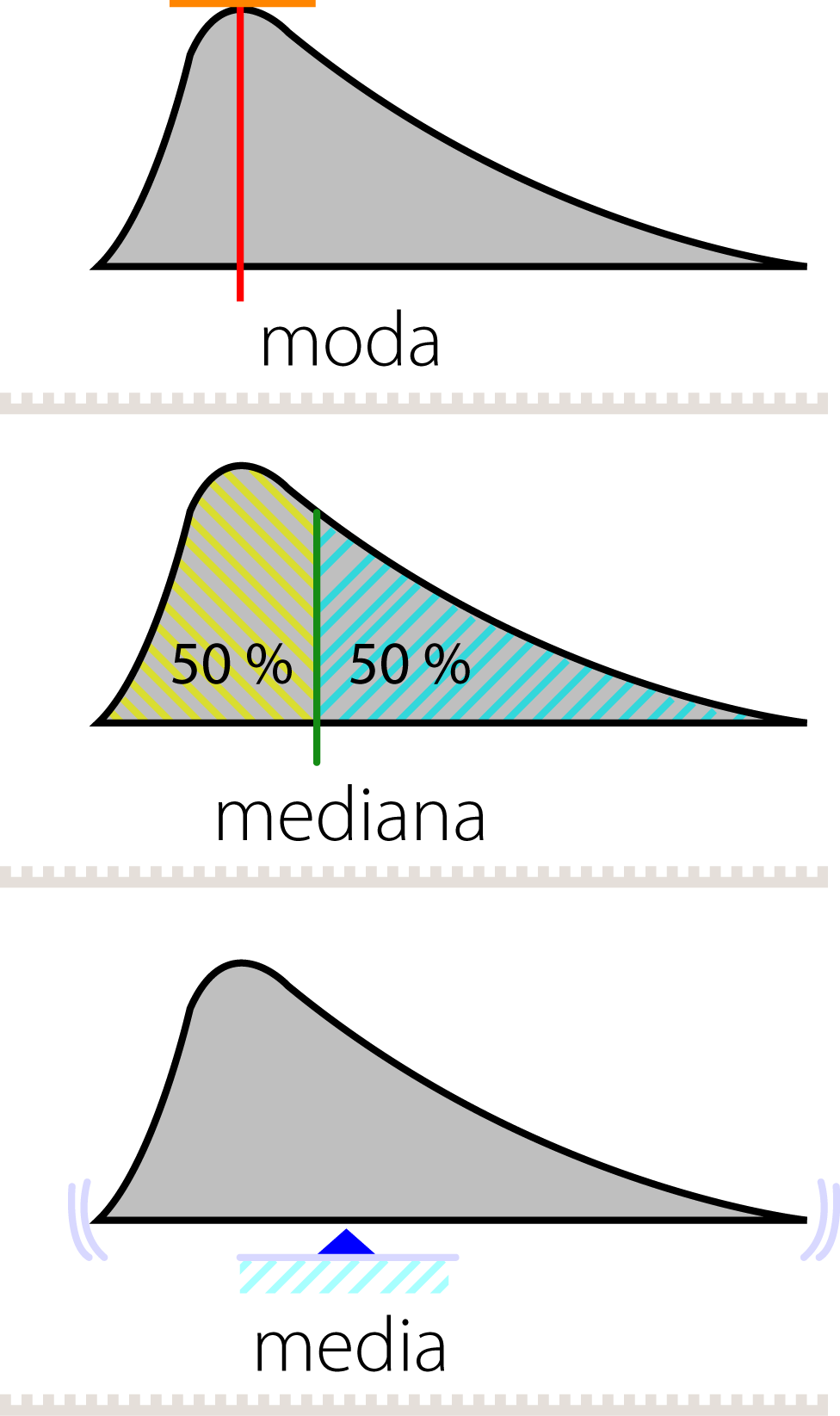
Antes de entrar en detalle con las medidas de tendencia central es importante entender que los datos pueden distribuirse de diferentes maneras. Algunas distribuciones son simétricas, en las que la media, la mediana y la moda coinciden en un mismo punto central. Otras distribuciones pueden ser asimétricas, en las que la media estará desplazada hacia un lado, mientras que la mediana y la moda se situarán en otro punto de la distribución.

A continuación, te explicaré con más detalle cada medida de tendencia central:

Media aritmética

La media aritmética es la suma de los valores de un conjunto de datos dividida por el número de datos. Esta medida de tendencia central es muy utilizada en la estadística y es especialmente útil cuando los datos están distribuidos de manera simétrica.

Consejos: Si los datos tienen valores extremos o valores muy dispersos, la media puede verse afectada y no ser representativa del conjunto de datos. Por esta razón, es importante tener en cuenta la dispersión de los datos al utilizar esta medida de tendencia central.

Mediana

La mediana es el valor que se encuentra en el centro del conjunto de datos cuando estos son ordenados de menor a mayor. Es decir, el 50% de los datos estarán por debajo de la mediana y el otro 50% estarán por encima de la mediana. Esta medida de tendencia central es muy útil cuando los datos están distribuidos de manera asimétrica.

Consejos: La mediana no se ve afectada por los valores extremos o los valores muy dispersos, por lo que es más representativa del conjunto de datos. Sin embargo, si el conjunto de datos es muy pequeño, la mediana puede no ser una buena representación del conjunto de datos.

Moda

La moda es el valor que aparece con mayor frecuencia en un conjunto de datos. Esta medida de tendencia central es muy útil cuando se quiere identificar cuáles son los valores más comunes del conjunto de datos.

Consejos: Al igual que la media, la moda puede verse afectada por los valores extremos o por los valores poco frecuentes presentes en el conjunto de datos. Por esta razón, es importante utilizar esta medida de tendencia central en conjunto con otras medidas de tendencia central para tener una visión más completa del conjunto de datos.

Cómo utilizar las medidas de tendencia central

Ahora que ya sabes qué son y cómo se calculan las medidas de tendencia central, es importante entender cómo utilizarlas para obtener información valiosa de un conjunto de datos. A continuación, te presento algunas ideas:

Identificar valores atípicos

Utilizando las medidas de tendencia central, es posible identificar valores atípicos o valores extremos dentro de un conjunto de datos. Si la media está muy alejada de la mediana y la moda, es probable que haya valores extremos que estén afectando el cálculo de la media. En este caso, es recomendable utilizar la mediana y la moda para tener una visión más clara del conjunto de datos sin que los valores extremos lo distorsionen.

Comparar conjuntos de datos

Las medidas de tendencia central también son útiles para comparar dos o más conjuntos de datos. Al comparar las medias de dos conjuntos de datos es posible identificar cuál de ellos tiene valores más altos o más bajos en promedio. Si los conjuntos de datos tienen distribuciones diferentes, es recomendable utilizar la mediana y la moda para una comparación más precisa.

Conclusiones

En conclusión, las medidas de tendencia central son una herramienta valiosa en la estadística y las matemáticas para entender la ubicación central de un conjunto de datos. La media aritmética, la mediana y la moda son las medidas de tendencia central más utilizadas y cada una de ellas tiene sus ventajas y desventajas dependiendo del conjunto de datos analizado. Recuerda siempre tener en cuenta la forma de distribución de los datos y utilizar varias medidas de tendencia central para obtener una visión más completa del conjunto de datos.

Espero que este artículo te haya sido útil y te haya permitido entender más sobre las medidas de tendencia central. ¡Hasta la próxima!