Moda y Estilo Las mejores ideas de Estilo de moda
¡Hola amigos y amigas! ¿Están listos para adentrarnos en el mundo de la estadística? ¡Hoy vamos a hablar de medidas de tendencia central en datos agrupados y no agrupados en el 2021!
Table of Contents
Medias de tendencia central
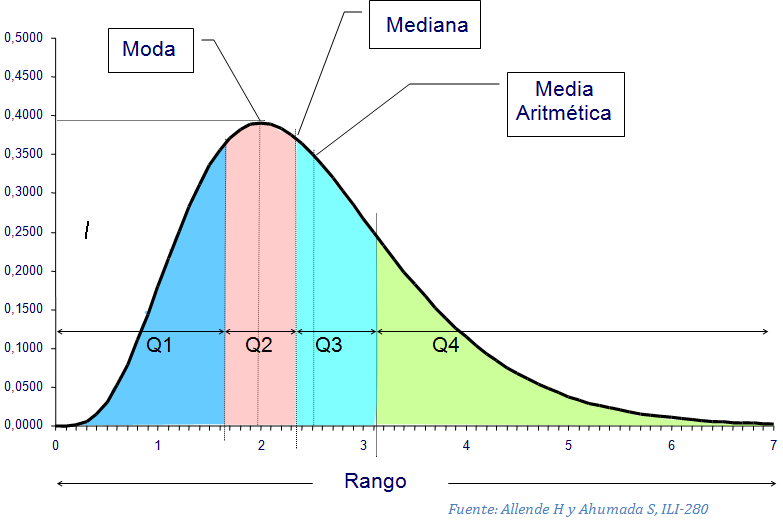
Comenzamos con uno de los conceptos más importantes y utilizados en estadística: las medidas de tendencia central. Estas medidas nos permiten resumir un conjunto de datos en un solo valor que represente el centro o punto medio del mismo. Las tres medidas más habituales son la media, la mediana y la moda.
La media se calcula sumando todos los valores de un conjunto de datos y dividiendo entre el número total de elementos. Es importante tener en cuenta que la media es muy sensible a los valores extremos, por lo que no representa bien la tendencia del conjunto de datos si existen valores atípicos.
La mediana es el valor central de un conjunto de datos ordenados de menor a mayor. Esta medida no se afecta por los valores extremos, por lo que representa mejor la tendencia de los datos.
Por último, la moda se refiere al valor que aparece con mayor frecuencia en un conjunto de datos. Es muy útil para datos no numericos o categoricos, pero puede haber varios valores modales o ninguno en algunos casos.
Tipos de datos
Los datos se pueden clasificar en dos tipos: agrupados y no agrupados. Los datos no agrupados son simples valores que se presentan en una lista, mientras que los agrupados se dividen en intervalos y se registran en forma de frecuencias.
En los datos no agrupados, la media, la mediana y la moda se calculan de la misma forma que hemos mencionado anteriormente.
En los datos agrupados, sin embargo, se debe considerar la frecuencia de cada intervalo para su cálculo. La media se calcula multiplicando el valor medio de cada intervalo por su respectiva frecuencia, y dividiendo entre el número total de datos. En el caso de la mediana, se debe construir la tabla de frecuencias acumuladas y buscar el valor central. La moda, por su parte, corresponde al valor del intervalo de mayor frecuencia.
Probabilidad y Estadística
En el ámbito de la probabilidad y la estadística, es muy común encontrar ejercicios y problemas que involucren medidas de tendencia central. Por ejemplo, podemos utilizarlas para resumir la edad de los estudiantes de una escuela, el tiempo que tarda un grupo de trabajadores en realizar una tarea, o los precios de un conjunto de productos.
Es importante recordar que, aunque las medidas de tendencia central nos dan una idea general de un conjunto de datos, no son suficientes para describir la totalidad de la distribución. Para ello, es necesario utilizar otras medidas o herramientas gráficas, como histogramas o boxplots.
¿Cómo aplicar estas medidas en nuestra vida cotidiana?
Ahora que ya sabemos qué son las medidas de tendencia central y cómo calcularlas, queremos compartir algunos consejos e ideas para aplicarlas en nuestra vida diaria.
Por ejemplo, podemos utilizar la media para conocer el gasto promedio en alimentos de una familia, o la mediana para saber cuál es el salario central en una empresa. La moda nos puede ayudar a identificar los productos más populares en un supermercado o las actividades preferidas en una comunidad.
También podemos utilizar estas medidas para evaluar nuestro rendimiento académico o laboral. Por ejemplo, podemos calcular la media de nuestras calificaciones en un semestre para tener una idea general de nuestro desempeño, o la mediana en el caso de que tengamos alguna calificación muy baja o muy alta que pueda afectar la media.
En conclusión, las medidas de tendencia central son una herramienta muy útil para resumir y analizar un conjunto de datos. Nos permiten comprender de manera sencilla la tendencia general de los mismos y tomar decisiones informadas. ¡Esperamos que este pequeño resumen les haya sido útil!
¡Hora de practicar!
Para poner en práctica lo que hemos aprendido, les proponemos algunos ejercicios sencillos:
1. Calcula la media, la mediana y la moda de los siguientes datos no agrupados: 10, 12, 9, 8, 11, 11, 12, 10, 8, 9.
2. A partir de la siguiente distribución agrupada de edades:
| Edad | Frecuencia |
|---|---|
| 18-25 | 20 |
| 26-33 | 15 |
| 34-41 | 10 |
| 42-49 | 5 |
Calcula la media, la mediana y la moda.
¡Esperamos que les hayan gustado estos ejercicios y que les hayan sido útiles para practicar!
¡A seguir aprendiendo!
Como podemos ver, las medidas de tendencia central son una herramienta muy útil para la estadística y la vida diaria. Pero esto es solo una pequeña introducción al mundo de la estadística. Si les interesa profundizar en el tema, les recomendamos buscar más información y ejercicios para seguir mejorando su conocimiento. ¡Nunca es tarde para aprender algo nuevo!
