Moda y Estilo Las mejores ideas de Estilo de moda
¡Hola amigos! Hoy hablaremos sobre las medidas de tendencia central en estadística. Las medidas de tendencia central son un conjunto de conceptos estadísticos que permiten conocer el valor central de una muestra de datos y proporcionar información sobre cómo se distribuyen los datos. En este artículo, vamos a ver algunas imágenes y explicaciones detalladas para que puedas entender este tema de manera fácil y efectiva.
Table of Contents
Medidas de Tendencia Central
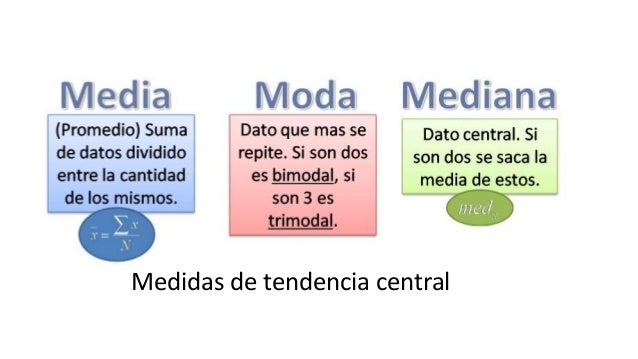
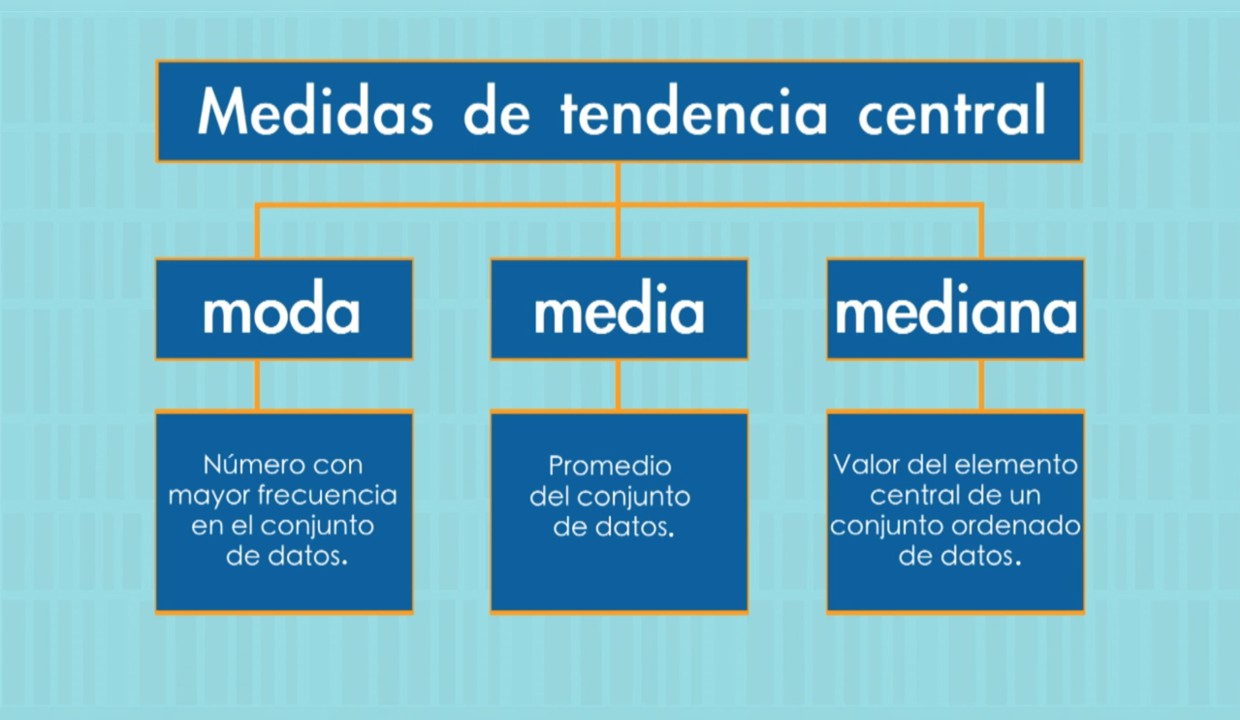
Las medidas de tendencia central son tres: media aritmética, mediana y moda.
La Media
La media aritmética es el valor central que se obtiene sumando todos los datos y dividiéndolos por el número total de datos. Es la medida de tendencia central más conocida y utilizada.
Consejos:
- La media es muy sensible a los valores extremos (outliers). Si hay outliers en los datos, la media no dará una representación adecuada de los datos.
- La media solo se puede calcular en datos numéricos continuos.
La Mediana
La mediana es el valor central de un conjunto de datos ordenados de menor a mayor. Si el número total de datos es impar, la mediana es el valor que ocupa la posición central. Si el número total de datos es par, la mediana es la media aritmética de los dos valores centrales.
Ideas:
- La mediana es más adecuada que la media cuando hay valores extremos.
- La mediana es muy útil para datos numéricos no continuos, como datos ordinales o discretos.
La Moda
La moda es el valor que se repite con más frecuencia en un conjunto de datos. Hay casos en los que no hay un valor que se repita con más frecuencia, entonces se dice que el conjunto de datos no tiene moda. Puede haber más de una moda si dos o más valores se repiten con la misma frecuencia.
Como calcular la moda:
La moda se puede calcular manualmente al contar la frecuencia de cada valor en un conjunto de datos y determinar cuál valor tiene la frecuencia más alta. También se puede utilizar una fórmula estadística para calcular la moda, pero esta última opción es más compleja.
Consejo:
La moda es muy útil para datos categóricos o nominales.
Conclusión
Las medidas de tendencia central son esenciales para cualquier estudio estadístico. Cada una de las tres medidas (media, mediana y moda) tiene ventajas y desventajas dependiendo del tipo de datos que se estén analizando, por lo que es importante probar todas las medidas y decidir qué medida es la más apropiada. Esperamos que este artículo haya sido útil y haya resuelto tus dudas sobre las medidas de tendencia central.
Como calcular las medidas de tendencia central
Calcular la media, mediana y moda es un proceso fácil. A continuación te explicamos cómo hacer cada uno:
Calculando la media
- Suma todos los valores de la muestra.
- Divide la suma por el número de valores.
- El resultado es la media.
Calculando la mediana
- Organiza los valores de la muestra en orden creciente o decreciente.
- Si la cantidad de valores es impar, la mediana es el valor central. Si es par, toma los dos valores centrales y calcula su media.
- El resultado es la mediana.
Calculando la moda
La moda se puede calcular manualmente al contar la frecuencia de cada valor en un conjunto de datos y determinar cuál valor tiene la frecuencia más alta.
También se puede utilizar una fórmula estadística para calcular la moda, pero esta última opción es más compleja. Si estás trabajando con un número elevado de datos o datos muy complejos, existe software específico que te puede ayudar a calcular la moda de forma sencilla.
Ideas finales
Las medidas de tendencia central son fundamentales para el análisis de datos en estadística. La media, mediana y moda son las medidas más comunes y conocidas, y cada una de ellas tiene su propia utilidad y limitaciones. Es importante considerar cada una de ellas y elegir la que mejor se adapte a la situación. Ahora ya sabes cómo calcular cada una de ellas, así que no dudes en aplicarlo en tus datos estadísticos. ¡Gracias por leer!
