En el análisis estadístico, es fundamental conocer las medidas de tendencia central para comprender mejor los datos obtenidos y obtener información precisa sobre la distribución de los mismos.
Table of Contents
Medidas de tendencia central
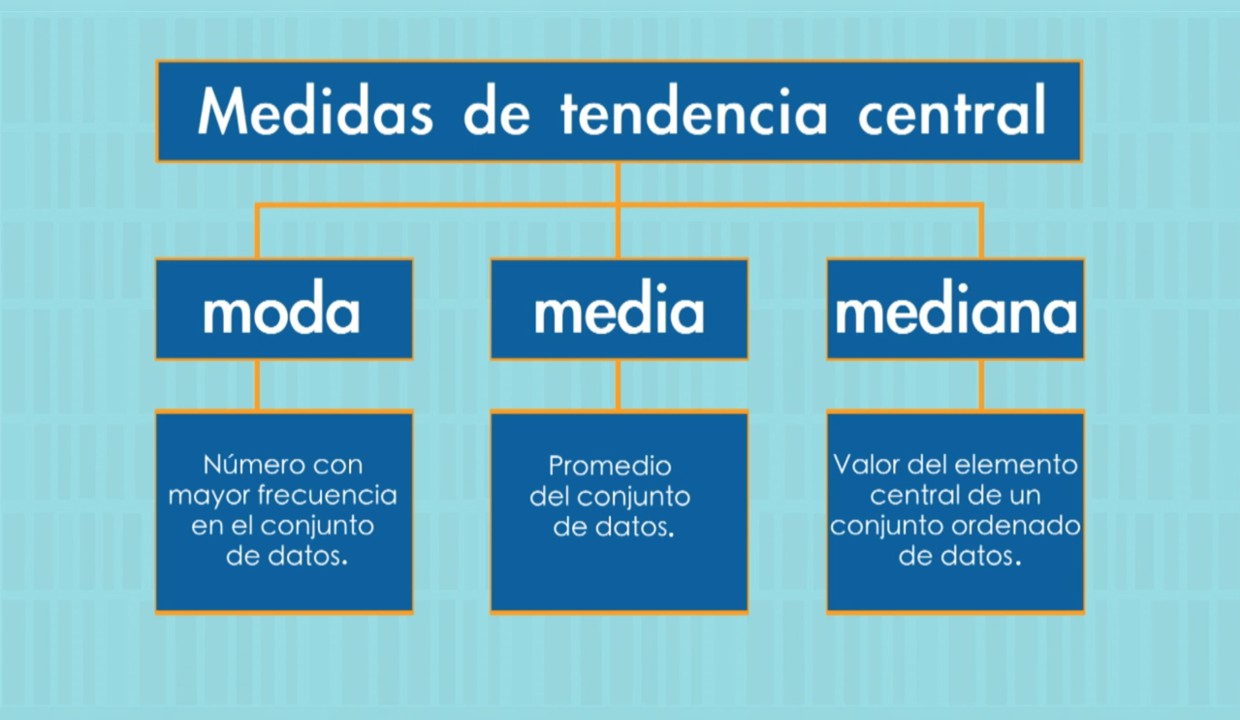
La media, mediana y moda son las medidas de tendencia central más comunes utilizadas para describir los datos. Cada una de ellas proporciona información valiosa acerca de los datos en una muestra o población.
Media
La media es la medida de tendencia central más común. Es simplemente el promedio de los datos en una muestra o población. Se calcula sumando todos los valores en la muestra y dividiendo el resultado por el número de observaciones en la muestra. La media es sensible a los valores atípicos, por lo que su uso debe realizarse con precaución.
Mediana
La mediana es la observación central en una muestra o población. Es el valor que divide a los datos ordenados en dos partes iguales. En otras palabras, la mitad de los datos son menores que la mediana y la otra mitad son mayores.

Moda
La moda es el valor que ocurre con mayor frecuencia en una muestra o población. En algunos casos, puede haber más de una moda si dos o más valores tienen la misma frecuencia máxima. La moda es útil para identificar picos o concentraciones en la distribución de los datos.
Consejos para el uso de las medidas de tendencia central
Para usar las medidas de tendencia central de manera efectiva, es necesario tener en cuenta varios factores importantes.
- Tener un conocimiento profundo del tipo de datos que se están analizando.
- Comprender la relación entre las diferentes medidas de tendencia central.
- Ser consciente de las limitaciones y los supuestos implícitos en cada medida.
- Tomar en cuenta la presencia de valores atípicos o datos extremos en la muestra.
- Interpretar los resultados de las medidas en el contexto de la pregunta de investigación o el problema que se está estudiando.
Ideas para el uso de las medidas de tendencia central en diferentes campos
Las medidas de tendencia central se utilizan en diversos campos para analizar y describir datos. Algunos ejemplos de cómo se pueden utilizar estas medidas en diferentes campos son los siguientes:
Economía
En la economía, las medidas de tendencia central se utilizan para analizar datos como ingresos, precios y producción. Por ejemplo, la media puede usarse para calcular el ingreso promedio de una población o el precio promedio de un producto en una región determinada.
Medicina
En la medicina, las medidas de tendencia central se utilizan para describir datos como la edad, el peso y las medidas biológicas. Por ejemplo, la mediana se utiliza a menudo para describir la edad de una población, ya que puede ser más representativa que la media, que puede ser afectada por valores atípicos como los bebés o los ancianos.
Psicología
En psicología, las medidas de tendencia central se utilizan para analizar datos como la inteligencia, la memoria y la personalidad. Por ejemplo, la moda puede utilizarse para describir la personalidad de una población determinada, identificando los rasgos que se repiten con más frecuencia.
Cómo calcular las medidas de tendencia central
Las medidas de tendencia central pueden calcularse de diferentes maneras, según la naturaleza de los datos y el tipo de análisis que se está realizando. Algunas de las formas más comunes de calcular las medidas de tendencia central incluyen:
Media aritmética
Como se mencionó anteriormente, la media aritmética es el promedio de los valores en una muestra o población. Puede calcularse sumando todos los valores en la muestra y dividiendo el resultado por el número de observaciones.

Mediana
La mediana puede obtenerse ordenando los valores de menor a mayor y seleccionando el valor central. Si hay un número par de valores, la mediana es la media de los dos valores centrales.
Moda
La moda puede obtenerse identificando el valor que se repite con mayor frecuencia en una muestra o población. Si hay varios valores que se repiten con frecuencia, hay varias modas.
En resumen, las medidas de tendencia central son una herramienta esencial para el análisis de datos en una amplia variedad de campos. Estas medidas proporcionan información valiosa sobre la distribución de los datos en una muestra o población, lo que permite a los investigadores realizar inferencias precisas y tomar decisiones informadas. Para utilizar estas medidas de manera efectiva, es necesario entender claramente sus posibilidades y limitaciones y aplicarlas de una manera cuidadosa y considerada.

Sin embargo, cabe destacar que el uso de estas medidas no es suficiente para obtener una visión completa del comportamiento de los datos. Además de las medidas de tendencia central, los investigadores deben también considerar otros aspectos importantes como la variabilidad, la dispersión y la simetría de los datos.
Conclusión
En la estadística, las medidas de tendencia central son esenciales para comprender y describir adecuadamente los datos que se estudian. La media, mediana y moda son técnicas que proporcionan información valiosa sobre la distribución de los datos y son ampliamente utilizadas en una amplia variedad de campos como la economía, la medicina, la psicología y muchas otras disciplinas.
El uso efectivo de estas medidas requiere un conocimiento profundo de los datos que se están analizando, así como una comprensión clara de las ventajas y limitaciones de cada medida. Además, el uso de las medidas debe realizarse de manera cuidadosa y considerada, teniendo en cuenta la presencia de valores atípicos y otros factores que puedan afectar la precisión de los resultados.
En resumen, el conocimiento y uso adecuado de las medidas de tendencia central son una habilidad valiosa para cualquier investigador que trabaje con datos, ya que permite la obtención de información precisa y confiable que es esencial para la toma de decisiones informadas y el análisis efectivo de los datos en cualquier campo.
 Moda y Estilo Las mejores ideas de Estilo de moda
Moda y Estilo Las mejores ideas de Estilo de moda


