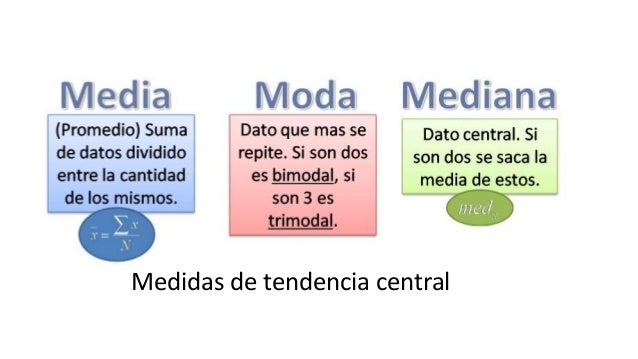
Las medidas de tendencia central son una herramienta fundamental en el análisis estadístico. Se utilizan para describir la forma en que los valores de una muestra se agrupan alrededor de un valor central. Existen tres medidas de tendencia central principales: la media, la mediana y la moda. A continuación, te contamos todo lo que necesitas saber para entenderlas mejor.
Table of Contents
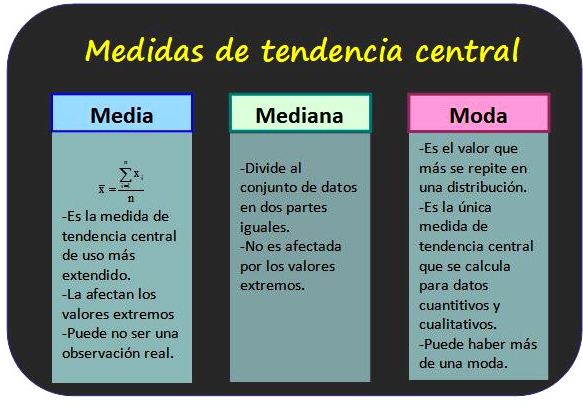
La media
La media es la medida de tendencia central más conocida y utilizada. Se calcula sumando todos los valores de la muestra y dividiéndolos por el número total de elementos. Es importante tener en cuenta que la media puede verse afectada por valores extremos (outliers). Esto puede generar una falsa impresión sobre el valor central de la distribución y reducir la fiabilidad de los resultados.
La mediana
La mediana es el valor que queda justo en el centro de una distribución ordenada de menor a mayor. Es el valor que divide la muestra en dos partes iguales. La mediana es más robusta a los valores extremos que la media. Por este motivo, se utiliza en aquellos casos en que los datos están muy dispersos o la muestra contiene valores atípicos.

La moda
La moda es el valor que aparece con mayor frecuencia en una distribución de datos. En otras palabras, es el valor más común. La moda es útil para describir distribuciones con valores categóricos, como el color de los ojos o la marca de un coche. Sin embargo, también puede utilizarse con valores numéricos.
Consejos para interpretar las medidas de tendencia central
A la hora de interpretar las medidas de tendencia central, es importante tener en cuenta algunos consejos para evitar errores en la interpretación de los datos:
- No confundir media con mediana: si la distribución es asimétrica, la media y la mediana serán diferentes.
- No utilizar la media si la distribución tiene valores extremos: para este tipo de distribuciones, la mediana es más adecuada.
- No utilizar la moda como medida de tendencia central única: en algunos casos, la moda puede no ser representativa del valor central de la distribución (por ejemplo, si hay dos o más modas).
Ideas para utilizar las medidas de tendencia central
Las medidas de tendencia central son útiles en muchas áreas del conocimiento. Aquí te presentamos algunas ideas para utilizarlas en diferentes campos:
- En economía: se utilizan para analizar la inflación, el crecimiento económico, el PIB, entre otros.
- En medicina: se utilizan para analizar parámetros clínicos, como la presión arterial, el colesterol, la glucemia, entre otros.
- En psicología: se utilizan para analizar resultados de tests psicológicos o encuestas.
- En deportes: se utilizan para analizar estadísticas de los jugadores, como el promedio de goles, asistencias o faltas cometidas.
Cómo calcular las medidas de tendencia central
Para calcular la media, se deben sumar todos los valores de la muestra y dividir el resultado por el número de elementos. En otras palabras:
media = (x1 + x2 + … + xn) / n
Para calcular la mediana, es necesario ordenar los valores y encontrar el valor que queda en el centro de la distribución. Si la muestra tiene un número impar de elementos, la mediana será el valor que queda exactamente en el centro. Si la muestra tiene un número par de elementos, la mediana será la media entre los dos valores que quedan en el centro.
Para calcular la moda, es necesario contar la frecuencia de cada valor de la muestra y encontrar el que se repite con mayor frecuencia. Si hay más de un valor que se repite con la misma frecuencia máxima, entonces la distribución es bimodal o multimodal.
En conclusión, las medidas de tendencia central son una herramienta clave en el análisis estadístico. Saber interpretarlas y utilizarlas de manera adecuada permite obtener conclusiones más precisas y confiables a partir de datos.
 Moda y Estilo Las mejores ideas de Estilo de moda
Moda y Estilo Las mejores ideas de Estilo de moda


