Que Es Moda Medidas De Tendencia

Las medidas de posición, de tendencia central y dispersión son una parte fundamental de la estadística descriptiva. Estas medidas permiten analizar y comprender mejor los datos y extraer información relevante para la toma de decisiones en diferentes campos. En este post te explicaremos las diferentes medidas de tendencia central y te daremos algunos consejos e ideas para su aplicación en la práctica.

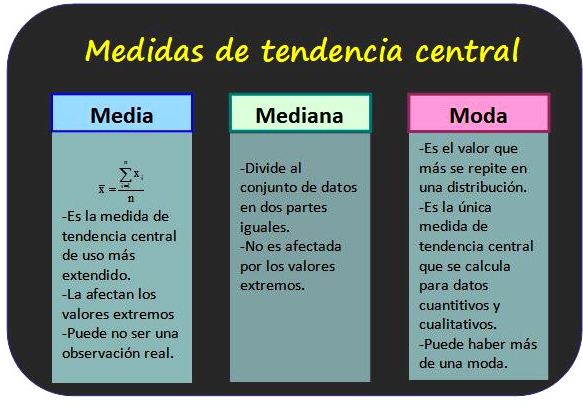
Medidas de tendencia central

Las medidas de tendencia central son aquellas que nos permiten encontrar un valor representativo alrededor del cual se agrupan los datos. Las tres medidas de tendencia central más utilizadas son:

• La media: es la suma de todos los valores dividida entre el número de datos.
• La mediana: es el valor central de un conjunto ordenado de datos. Si la serie de datos es impar, la mediana es el valor central. Si es par, se toma la media de los dos valores centrales.
• La moda: es el valor más frecuente en un conjunto de datos.

A continuación, te mostramos algunos consejos para su aplicación en la práctica.

Consejos

1. Compara la media y la mediana: La media es sensible a valores extremos y puede ser influenciada por ellos. La mediana, por otro lado, es más resistente a estos valores y puede ser una mejor medida de tendencia central en estos casos.

2. Utiliza la moda en datos nominales o categóricos: La moda es una buena medida de tendencia central para datos nominales o categóricos, donde no se pueden calcular la media o la mediana.

3. Considera el contexto: La elección de la medida de tendencia central más adecuada depende del contexto en el que se esté trabajando. Por ejemplo, en un examen en el que la nota más frecuente fue un suspenso, la media no sería una buena medida de rendimiento.

Ideas

1. Analiza la distribución de tus datos: Antes de elegir una medida de tendencia central, es importante analizar la distribución de los datos. Si los datos tienen una distribución normal, la media es una buena opción. Si la distribución no es simétrica o hay valores extremos, es mejor utilizar la mediana o la moda.

2. Utiliza diferentes medidas de tendencia central para un análisis más completo: Es posible que diferentes medidas de tendencia central lleguen a conclusiones diferentes en cuanto a los datos. Por eso, utilizar varias medidas de tendencia central puede proporcionar un análisis más completo.

3. Considera la dispersión de los datos: Las medidas de tendencia central no proporcionan información sobre la dispersión de los datos. Para entender completamente la distribución de los datos, es necesario considerar la dispersión. Algunas medidas de dispersión son la varianza y la desviación estándar.

¿Cómo calcular las medidas de tendencia central?

El cálculo de las medidas de tendencia central es sencillo. A continuación, te explicamos cómo calcular cada una de ellas:

Media: La media se calcula sumando todos los valores y dividiendo entre el número de datos:

Mediana: Para calcular la mediana, es necesario ordenar los datos de menor a mayor y encontrar el valor central:

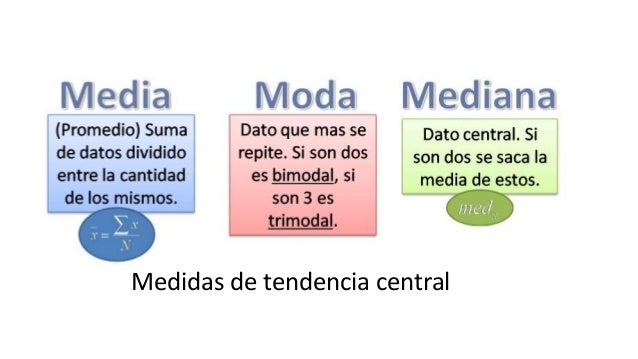
Moda: La moda es el valor más frecuente en un conjunto de datos:

En resumen, las medidas de tendencia central son una herramienta importante en la estadística descriptiva y permiten analizar los datos de una manera más profunda. Es importante tener en cuenta el contexto y la distribución de los datos para elegir la medida de tendencia central más adecuada. Además, es recomendable considerar la dispersión de los datos y utilizar varias medidas de tendencia central para un análisis más completo.