Que Significa Medida De Tendencia Central Moda

¡Hola familia! ¿Cómo están? Hoy les traigo información súper útil y necesaria en nuestro día a día, especialmente en el ámbito académico y laboral. Se trata de las medidas de tendencia central, un concepto que puede sonar un poco complicado, pero que es esencial para entender y analizar datos y estadísticas. ¡No se preocupen que aquí les explico todo con detalle!

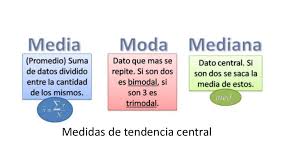
¿Qué son las medidas de tendencia central?

Las medidas de tendencia central son un conjunto de valores estadísticos que representan la tendencia de un conjunto de datos hacia una posición central. Lo que esto quiere decir es que nos dan una idea de cuál es el valor promedio o típico de un conjunto de datos, es decir, dónde se agrupan la mayoría de los valores.

Existen tres medidas de tendencia central principales: la media aritmética, la mediana y la moda. Cada una tiene una forma particular de calcularse y proporciona información valiosa sobre los datos que se están analizando.

Media aritmética

La media aritmética es la medida más común y conocida de tendencia central. Se calcula sumando todos los valores de un conjunto de datos y dividiendo el resultado entre el número total de valores. Es decir, si tenemos el conjunto de datos 2, 4, 6, 8, 10, su media aritmética sería:

(2 + 4 + 6 + 8 + 10) ÷ 5 = 30 ÷ 5 = 6

En este caso, la media aritmética del conjunto de datos es 6, lo que significa que este valor representa el valor promedio o típico de los datos.

Consejo: La media aritmética es muy útil para analizar datos cuantitativos, como la edad, la estatura o el precio de un producto. Sin embargo, puede ser influenciada por valores extremos o atípicos, por lo que es importante analizar el conjunto de datos completo para evitar interpretaciones erróneas.

Mediana

La mediana es otra medida de tendencia central que se calcula a partir de un conjunto de datos. La mediana es el valor que se encuentra en el centro de los datos ordenados de menor a mayor o de mayor a menor. Es decir, si tenemos el conjunto de datos 2, 4, 6, 8, 10, la mediana sería el valor que se encuentra justo en el medio, es decir, el valor de la posición 3, que es 6.

Es importante destacar que la mediana solo se ve afectada por los valores que se encuentran en el centro del conjunto de datos, lo que la hace más resistente a valores extremos o atípicos que la media aritmética.

Idea: La mediana es especialmente útil cuando los datos presentan una distribución asimétrica, es decir, cuando hay una mayor cantidad de valores concentrados en un extremo del conjunto de datos que en el otro. En estos casos, la media aritmética puede ser engañosa, mientras que la mediana proporciona una visión más precisa de los datos.

Moda

Por último, tenemos la moda, que es la medida de tendencia central que representa el valor que ocurre con mayor frecuencia en un conjunto de datos. Es decir, si tenemos el conjunto de datos 2, 2, 4, 6, 6, 8, 8, 8, 10, 10, la moda sería el valor 8, que aparece tres veces en el conjunto de datos.

Al igual que la mediana, la moda no se ve influenciada por valores extremos o atípicos en el conjunto de datos.

Como: La moda es una medida de tendencia central muy útil para analizar datos cualitativos, que corresponden a características no numéricas, como el género, el color preferido o el tipo de trabajo.

Conclusión

Como pueden ver, las medidas de tendencia central son un concepto muy importante y útil para analizar y entender un conjunto de datos. Cada una de las tres medidas principales (media aritmética, mediana y moda) proporciona información valiosa sobre los datos que se están analizando, pero es importante tener en cuenta las particularidades de cada una para evitar malinterpretaciones y conclusiones erróneas.

Espero que esta información haya sido útil y les haya ayudado a entender mejor las medidas de tendencia central. No olviden aplicarlas en su vida cotidiana y en sus proyectos académicos y laborales. ¡Hasta la próxima familia!