
¡Hola mi gente! ¿Cómo están? Hoy quiero hablarles sobre un tema muy interesante que es la estadística y las medidas de tendencia central. Aunque puede sonar aburrido, esta herramienta es muy útil para analizar y comprender información importante. Así que sin más preámbulos, ¡empecemos!
Table of Contents
Medidas de tendencia central
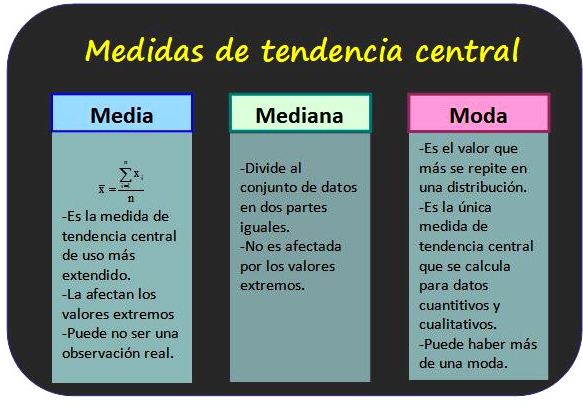
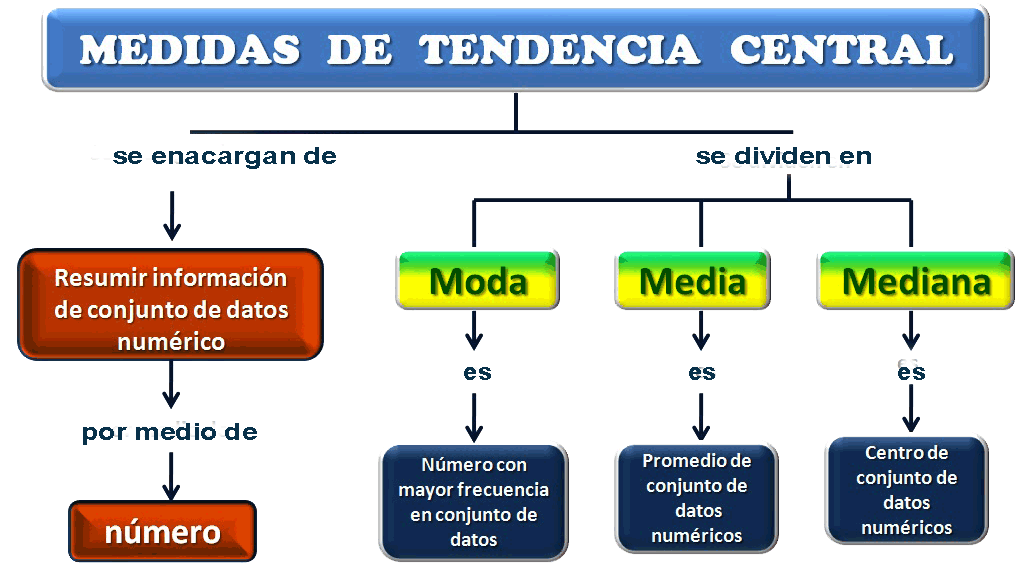
Las medidas de tendencia central son una forma de resumir y representar una distribución. Estas medidas nos ayudan a entender y analizar datos de una forma más fácil. Las medidas más comunes son la media, la mediana y la moda.
Media
La media es la suma de todos los datos divididos por el número de datos. Es una medida de tendencia central muy común y representa el punto de equilibrio de los datos. Para calcular la media, se suman todos los valores y se dividen por el número total de valores.
Por ejemplo, si queremos calcular la media de las edades de un grupo de personas, debemos sumar todas las edades y dividir por el número de personas.
Consejos para calcular la media
- Asegúrate de que tienes todos los valores correctos y completos.
- Agrega todos los valores y divide por el número total de valores.
- Comprueba que el resultado es lógico y representativo.
Mediana
La mediana es el valor que ocupa la posición central en un conjunto de datos ordenados. Es decir, si ordenamos los datos de menor a mayor, la mediana será el valor que está justo en el centro. Si hay un número impar de valores, la mediana es el valor central. Si hay un número par de valores, la mediana es la media de los dos valores centrales.

Consejos para calcular la mediana
- Ordena los datos de menor a mayor.
- Encuentra el valor central.
- Si hay un número impar de valores, la mediana es el valor central.
- Si hay un número par de valores, la mediana es la media de los dos valores centrales.
- Comprueba que el resultado es lógico y representativo.
Moda
La moda es el valor que aparece con mayor frecuencia en un conjunto de datos. Es decir, es el valor que se repite más veces. Puede haber una moda (un valor que se repite más que cualquier otro) o puede haber varias modas (varios valores que se repiten con la misma frecuencia).

Consejos para calcular la moda
- Identifica el valor que se repite más veces.
- Si hay varios valores que se repiten con la misma frecuencia, hay varias modas.
- Comprueba que el resultado es lógico y representativo.
Dispersión
Además de las medidas de tendencia central, también es importante analizar la dispersión de los datos. La dispersión es una medida de cuánto se alejan los datos del valor central. Las medidas más comunes son la desviación estándar, la varianza y el rango.

Desviación Estándar
La desviación estándar es una medida de dispersión que indica cuánto se alejan los datos del valor central. Es la raíz cuadrada de la varianza y se expresa en las mismas unidades que los datos. Una desviación estándar grande indica que los datos están muy dispersos, mientras que una desviación estándar pequeña indica que los datos están muy juntos.
Consejos para calcular la desviación estándar
- Calcula la media.
- Calcula la diferencia entre cada dato y la media.
- Calcula el cuadrado de cada diferencia.
- Suma los cuadrados de las diferencias.
- Divide la suma por el número de datos.
- Saca la raíz cuadrada del resultado.
- Comprueba que el resultado es lógico y representativo.
Varianza
La varianza es una medida de dispersión que indica cuánto se alejan los datos del valor central. Es la media de los cuadrados de las diferencias entre cada dato y la media. Una varianza grande indica que los datos están muy dispersos, mientras que una varianza pequeña indica que los datos están muy juntos.
Consejos para calcular la varianza
- Calcula la media.
- Calcula la diferencia entre cada dato y la media.
- Calcula el cuadrado de cada diferencia.
- Suma los cuadrados de las diferencias.
- Divide la suma por el número de datos.
- Comprueba que el resultado es lógico y representativo.
Rango
El rango es una medida de dispersión que indica la diferencia entre el mayor y el menor valor en un conjunto de datos. Es una medida muy simple de dispersión, pero también es muy sensible a valores extremos. Un rango grande indica que los datos tienen una gran variabilidad, mientras que un rango pequeño indica que los datos tienen poca variabilidad.
Consejos para calcular el rango
- Encuentra el valor máximo y el valor mínimo.
- Calcula la diferencia entre el valor máximo y el valor mínimo.
- Comprueba que el resultado es lógico y representativo.
Cómo usar las medidas de tendencia central
Las medidas de tendencia central son muy útiles para comprender y analizar un conjunto de datos. Estas medidas nos permiten resumir y representar los datos de una forma más fácil y comprensible. Algunas de las principales aplicaciones de las medidas de tendencia central incluyen:
Identificar la tendencia central
La media, la mediana y la moda son herramientas muy útiles para identificar la tendencia central de un conjunto de datos. Estas medidas nos ayudan a entender cuál es el valor central alrededor del cual se agrupan los datos.
Comparar diferentes conjuntos de datos
Las medidas de tendencia central también nos permiten comparar diferentes conjuntos de datos. Por ejemplo, si queremos saber cuál es la edad promedio de los estudiantes en dos escuelas diferentes, podemos calcular la media de cada conjunto de datos y comparar los resultados.
Evaluar la dispersión
Además de identificar la tendencia central, las medidas de tendencia central también nos permiten evaluar la dispersión de los datos. Esto es importante para entender la variabilidad de los datos y proporciona información valiosa para la toma de decisiones.
Consejos finales
Espero que este artículo les haya sido útil y hayan aprendido un poco más sobre las medidas de tendencia central. Recuerden que la estadística es una herramienta muy útil en muchos campos y puede ayudarnos a comprender mejor el mundo que nos rodea.
Recuerden también que las medidas de tendencia central son solo una parte del análisis estadístico y que es importante evaluar la dispersión de los datos para obtener una imagen completa.
¡Hasta la próxima, mi gente!

PD: Si quieren más información sobre este tema, echénle un vistazo a este recurso que encontré en la red.
Y para aquellos interesados en profundizar aún más en este tema, les recomiendo leer este blog, que contiene información detallada sobre la estadística y las medidas de tendencia central.

Como siempre, recuerden que la educación es poder y que siempre es bueno aprender cosas nuevas. ¡Hasta la próxima!
 Moda y Estilo Las mejores ideas de Estilo de moda
Moda y Estilo Las mejores ideas de Estilo de moda

